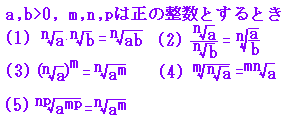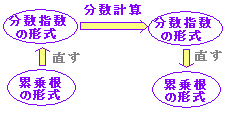
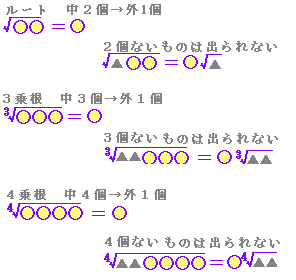
累乗根

※高校数学Ⅱの「指数関数」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

== 累乗根 == 【解説】
■ｎ乗根の定義
　ｎ乗してａになる元の数をａのｎ乗根といい，で表わします。

X^{n} = a (a > 0)

となる元の数Xをaのn乗根といい，

\sqrt[n]{a}

で表す．
すなわち，

［累乗根の定義］：

X^{n} = a \leftarrow\to X = \sqrt[n]{a}

（覚え方：漫才コンビの荷物）
Xが肩の荷物を降ろして楽になると，相方aの手のひらに荷物が乗る．→

\sqrt[n]{a}

　特に，n=2の場合だけnを省略してと書きます。

(　は　　ではなく，　を表わします。)

【例】
2³=8　だから　=2
3²=9　だから　=3　(省略すれば２乗根)

　だから　

(-2)⁵=-32　だから　

■次のグラフから分かるように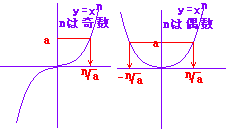　

(1)　ｎが奇数のとき　ｘ^ｎ=ａ　となるｘの値は，ａの正負によらず常にただ１つ存在し、この値を

で表わします。
(2)　ｎが偶数のときはａ＞0のとき，　ｘ^ｎ=ａ　となるｘの値は，２つ存在しますので，そのうち正の値を

で，負の値を-

で表わします。ａ＜０のときは，ｘ^ｎ=ａ　となるｘの値はありません。

※　ａ＞０の範囲で考える限り，ｎが奇数でも，偶数でも　ｘ^ｎ=ａ　となるｘの値は，ただ１つ存在し、その値がです。
このページでは，以下においてａ＞０のみ扱います。

■累乗根の性質

■解説

【例】
(1)　

\sqrt[3]{2} \sqrt[3]{3} = \sqrt[3]{6}

，

\sqrt[3]{2} \sqrt[3]{4} = \sqrt[3]{8}

= \sqrt[3]{2^{3}} = 2

(2)　

\frac{\sqrt[3]{4}}{\sqrt[3]{2}} = \sqrt[3]{\frac{4}{2}} = \sqrt[3]{2}

，

\frac{\sqrt[4]{96}}{\sqrt[4]{6}} = \sqrt[4]{\frac{96}{6}} = \sqrt[4]{16} = \sqrt[4]{2^{4}} = 2

(3)　

(\sqrt[3]{2})^{6} = (\sqrt[3]{2}) (\sqrt[3]{2}) (\sqrt[3]{2}) \times (\sqrt[3]{2}) (\sqrt[3]{2}) (\sqrt[3]{2}) = 2^{2}

\sqrt[3]{2^{6}} = \sqrt[3]{2^{2} \times 2^{2} \times 2^{2}} = 2^{2}

だから

(\sqrt[3]{2})^{6} = \sqrt[3]{2^{6}}

(4)　

\sqrt{\sqrt[3]{64}} = \sqrt{\sqrt[3]{4^{3}}} = \sqrt{4} = 2

\sqrt[6]{64} = \sqrt[6]{2^{6}} = 2

だから

\sqrt{\sqrt[3]{64}} = \sqrt[6]{64}

ここで

\sqrt{a}

は

\sqrt[2]{a}

であることに注意
(5)　

(\sqrt[6]{2^{4}})^{6} = 2^{4}

(\sqrt[3]{2^{2}})^{6} = 2^{2} \times 2^{2} = 2^{4}

だから

\sqrt[6]{2^{4}} = \sqrt[3]{2^{2}}

※重要※
上記の累乗根の性質(1)～(5)のうち単純なものは使いますが，後に登場する分数指数を用いた計算の方が楽です。
　教科書においても，累乗根の性質の練習問題は取り扱いが薄いようです。
　ただし，問題と解答は累乗根形式に指定されていることがあります。

※筆者おすすめの方法※

■要点■ $\sqrt[n]{a^{n}} = a$ 　(a>0) $X^{n} = a (a > 0)$ となる元の数Xをaのn乗根といい， $\sqrt[n]{a}$ で表す．すなわち，［累乗根の定義］： $X^{n} = a \leftarrow\to X = \sqrt[n]{a}$ これを右辺が $a^{n} (a > 0)$ の場合に適用すると $X^{n} = a^{n} \to X = \sqrt[n]{a^{n}}$ $↓$ $X = a$ したがって $\sqrt[n]{a^{n}} = a$
※以下では，極簡単なものだけを取り上げています。複雑な計算問題は，上の解説でも述べたように「分数指数」で行う方が有利です。【問題１】　左の式の値に等しいものを右から選びなさい．左から一つクリックし，続けて右から「対応するもの」をクリックすると，正答なら問題と答が消えます．正答の場合でも誤答の場合でも，解答すれば［解説］というボタンが出ますので，答を確かめることができます．

解説 $\sqrt[3]{8} = \sqrt[3]{2^{3}} = 2$ $\sqrt[4]{81} = \sqrt[4]{3^{4}} = 3$ $\sqrt[3]{\frac{1}{64}} = \sqrt[3]{(\frac{1}{4})^{3}} = \frac{1}{4}$ $\sqrt[5]{100000} = \sqrt[5]{10^{5}} = 10$ $\sqrt[3]{54} = \sqrt[3]{2 \times 3^{3}} = 3 \sqrt[3]{2}$ $\sqrt[4]{\frac{81}{16}} = \sqrt[4]{(\frac{3}{2})^{4}} = \frac{3}{2}$ $\sqrt[3]{\frac{32}{27}} = \sqrt[3]{\frac{2^{5}}{3^{3}}} = \frac{2}{3} \sqrt[3]{2^{2}} = \frac{2}{3} \sqrt[3]{4}$ →閉じる←

【問題２】　ｘ，ｙ＞0のとき，左の式の値に等しいものを右から選びなさい．左から一つクリックし，続けて右から「対応するもの」をクリックすると，正答なら問題と答が消えます．正答の場合でも誤答の場合でも，解答すれば［解説］というボタンが出ますので，答を確かめることができます．

解説 $\sqrt[3]{x^{3} y^{2}} = x \sqrt[3]{y^{2}}$ $\sqrt[3]{x y^{3}} = y \sqrt[3]{x}$ $\sqrt[4]{x^{6} y^{3}} = x \sqrt[4]{x^{2} y^{3}}$ $\sqrt[4]{x^{2} y^{5}} = y \sqrt[4]{x^{2} y}$ $\sqrt[5]{x^{10} y^{6}} = x^{2} y \sqrt[5]{y}$ $\sqrt[5]{x^{5} y^{11}} = x y^{2} \sqrt[5]{y}$ $\sqrt[3]{x^{4} y} = x \sqrt[3]{x y}$ →閉じる←