|
簡単に言えば,累乗根は累乗の逆を表します.(累乗は2乗,3乗,4乗,…の総称です.累乗根は2乗根,3乗根,4乗根,…の総称です.)
例
32=9 → =3 …(*) 53=125 → =5 24=16 → =2 は2乗根と呼ばれます. は3乗根と呼ばれます. … はn乗根と呼ばれます. ※中学校のときには,平方根はプラスとマイナスの2つあるということを強調するために,aの平方根は±,aのルートはというように厳格に区別しましたが,高校では単にをn乗根というだけです. |
|
=  これは,中学校で習ったとき以来の約束事ですが,ここでは,のように省略されたら,
でもなく
でもなく
を表すということが重要. これは,中学校で習ったとき以来の約束事ですが,ここでは,のように省略されたら,
でもなく
でもなく
を表すということが重要.すぐ後で述べるように,この数字は「分数の指数」に直したときに分母になります. |
|
•a>0であってnが正の偶数のとき,
xn=a →2つの実数xがこの方程式の解になります.
•a>0であってnが正の奇数のとき,そのうちの正の実数はで表されます. 負の値の方は−で表されます.
xn=a →ただ1つの正の実数xがこの方程式の解になります.
•a<0であってnが正の偶数のとき,この正の実数はで表されます.
xn=−a →この方程式には実数解xはありません.
•a<0であってnが正の奇数のとき,
xn=−a →ただ1つの負の実数xがこの方程式の解になります.
•a=0のときは,nが偶数であっても奇数であってもこの負の実数はで表されます.
xn=0 → x=0です.
=0(1つの値になります.)
以下においては,累乗根の根号内は正の数だけを考え,その正の累乗根だけを考えます.
したがって,nが偶数でも奇数でも各々のa, nに対しては,ただ1つの正の実数を表します. (右図の青で示した○の部分) |
次の図から分かるように,y=xnのグラフは,nが偶数の場合と奇数の場合で違う形になります.このため,y=xnの逆(a=xnとなるようなxの値を求める操作)は偶数の場合と奇数の場合で分けて考える必要があります.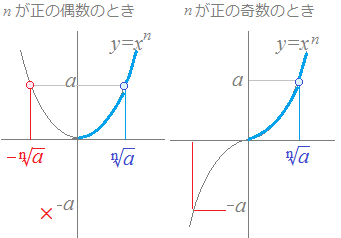 |
|
≪n乗根の計算法則≫ n乗根の根号内がn以上のときは,累乗根の記号を簡単にすることができます.
=a
(解説)bが整数のn乗の形に書けないとき =a 累乗根の定義から xn=a → x= したがって x=a (a>0)のとき xn=an → x= ∴=a |
|
例 (1)==2 (2)==2 (累乗根記号で「手のひら」(♪〜これはこの教材の中だけの言い方.全国共通ではないので注意.)の数字が省略されているものは2乗根を表します) (3)===2 (4)==5 (5)==2 (6)==2 |
