|
== 分数関数 ==
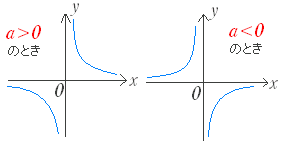
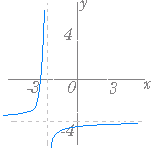
■解説 ○ 中学校で習う反比例の関数 は右図1のような直角双曲線である.(直角双曲線の「直角」とは,漸近線が直角に交わるということで,直角でない双曲線は数学Cで学ぶ.) 【 グラフの平行移動 】 ・・・(1)
一般に,関数  【 直角双曲線の平行移動 】 ・・・(2)
関数 y= のグラフを x 軸の正の向きに p, y 軸の正の向きに q だけ平行移動してできるグラフの方程式は y=+q になる. |
図1
 (1)の詳しい解説→ (2)の例: y=+4 のグラフは,y= のグラフを x軸の正の向きに 2,y 軸の正の向きに 4 だけ平行移動したものだから,次のようなグラフになる. 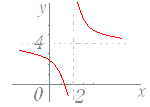 |
|
【 漸近線の方程式 】 ・・・(3)
y=+q の漸近線の方程式は,x=p 及び y=q ※ グラフが限りなく近づく線(直線)を漸近線という.この場合,グラフは漸近線に限りなく近づくが,漸近線と交わったり接したりすることはない. 例えば,y=q が漸近線であるとき,x のどのような値に対しても y=q となることはない. また,x=p が漸近線であるとき, x=p の値に対応する点はない. ※ したがって,y=+q のグラフでは,x≠p 及び y≠q となる. |
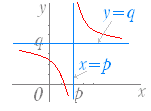 値域は y<q , q<y |
|
【 xy=a の形での表示 】 ・・・(4)
関数 は,分母を払えば xy=a と同じである.この形で書かれることもある,そのとき,平行移動や漸近線の公式は次の通り. xy=a のグラフを x 軸の正の向きに p, y 軸の正の向きに q だけ平行移動してできるグラフの方程式は |
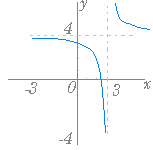
例 2xy−4x+3y−2=0 は (2x+3)(y−2)+6−2=0 と変形すると (2x+3)(y−2)=−4 すなわち,(x+)(y−2)=−−2 となるから xy=−2 のグラフを x 軸の正の向きに −, y 軸の正の向きに 2 だけ平行移動グラフで, 漸近線の方程式は x=− , y=2 となる. |
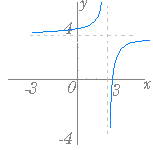
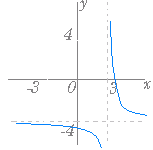
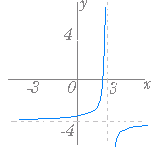
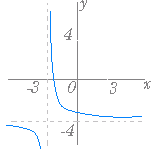
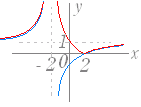 (1)
(1) 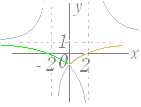 (2)
(2)