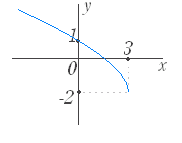|
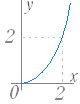
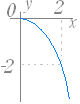
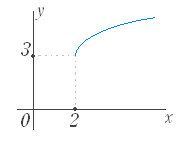
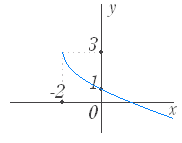
■無理関数 ■解説 ○ 無理関数のグラフ (1) y= ( a>0,定義域:x≧0,値域:y≧0 ) のグラフは右図1のようになる.
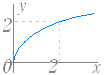
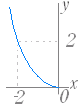
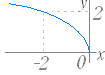
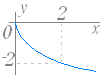
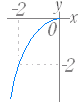
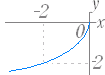
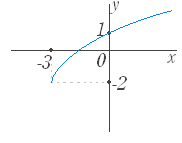
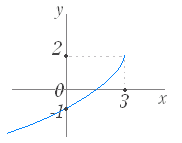
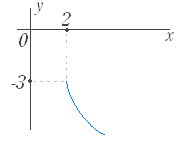
のグラフは y= のグラフを x 軸に関して対称に移動したもので右図2のようになる. (3) y= ( a>0,定義域:x≦0,値域:y≧0 ) のグラフは y= のグラフを y 軸に関して対称に移動したもので右図3のようになる. (4) y=− ( a>0,定義域:x≦0,値域:y≦0 ) のグラフは y= のグラフを原点に関して対称に移動したもので右図4のようになる. |
図1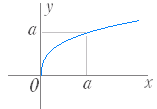 図1’
図1’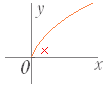 図2 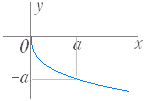 図3
図3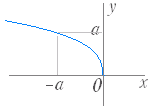 図4 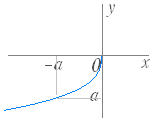
|
| ○ 無理関数のグラフの平行移動 (1) y= のグラフを x 軸の正の向きに p, y 軸の正の向きに q だけ平行移動してできるグラフの方程式は, y= +q になる. 元のグラフが,y=− , y= , y=− のときも同様 |
※ グラフの平行移動の基本については,このページ参照 例 y= +3 のグラフ 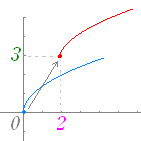 y=−2 のグラフ 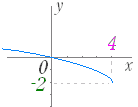 y= のグラフを描くときは,y= に変形して考えるとよい. 例 y=2 のグラフを描くときは,y= に変形して考えるとよい. |