|
ウ 条件・集合の問題 |
|
1
pはqであるための必要条件,
qはrであるための十分条件 であるとき, pであることはrであるための( )条件 |
ヒント↓  |
 |
| 2
pはqであるための必要条件,
qはrであるための必要十分条件, sはrであるための十分条件 であるとき, sはpであるための( )条件 |
ヒント↓  |
 |
| 3
pはqであるための必要条件,
qはrであるための必要条件, rはsであるための必要条件, sはpであるための必要条件 であるとき, rはpであるための( )条件 |
ヒント↓  |
 |
| 4
pはqであるための十分条件,
qはrであるための十分条件, rはsであるための十分条件, sはqであるための十分条件 であるとき, sはpであるための( )条件 |
ヒント↓  |
 |
| 5
C⊂AまたはC⊂B であることは,
C⊂A∪B であるための( )条件 |
ヒント↓  |
 |
| 6
A∩B⊃A∪B であることは,
A=B であるための( )条件 |
ヒント↓  |
 |
| 7
A∪C⊃B∪C となるCが存在することは,
A⊃B であるための( )条件 |
ヒント↓  |
 |
| 8
A∩B≠
A∩B∩C≠ |
ヒント↓ 
|  |
| 9
すべてのCについてA∩C⊃B∩C となることは,
A⊃B であるための( )条件 |
ヒント↓
すべてのCについて(どんなCについても)成り立つならば,当然ある特定のCについても成り立たなければなりません.だから,例えばC=U(全体集合)である場合,C=φ(空集合),C=A,C=Bである場合にも成り立たなければなりません.
つまり,「すべてのCについて○○」に対して「あるCについて○○」は必要条件になります. そこで,いくつかのCについてこのような必要条件を試してみて,捜査の範囲を絞ります.特にC=U(全体集合)とき,A⊃Bとなり,これが必要条件です.(この問題では,他の場合に得られる結論は当然成り立つものばかりです) 次に,A⊃Bのとき,「すべてのCについてA∩C⊃B∩C」となるかどうか調べます.(十分条件が成り立っているかどうかを調べます) A⊃Bのときは次の図において×印の箇所がないので「すべてのCについてA∩C⊃B∩Cとなる」ことがいえます.(十分条件も成立します) 問題文では「すべてのCについてA∩C⊃B∩C」となることを主語としているので,上記の論理と主客を反対に答えて,前半では十分条件,後半では必要条件が成立していることになります. 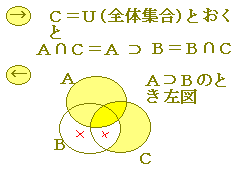
|
 |
| 10
A⊃B,B⊃C,C⊃A は,
A=B=C であるための( )条件 |
ヒント↓  |
 |
| 11
次の 命題「PならばQ」がなりたつとする.このとき,命題「PならばR」が成り立つことは,命題「QならばR」がなりたつための
(1) 必要十分条件である (2) 必要条件であるが,十分条件とは限らない (3) 十分条件であるが,必要条件とは限らない (4) 必要条件とも,十分条件とも限らない ・・・・「東京理科大学 S57年度入試問題」の引用
|
(1) (2) (3) (4)
ヒント↓ 
(1) (2) (3) (4) ヒント↓  |

|