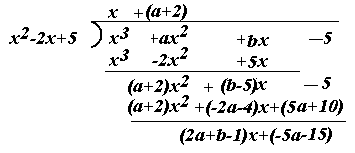|
→ 携帯用は別頁
【要点】 係数が実数である方程式が虚数解をもつと,なぜうれしいのか?
<例>
係数が実数であるような方程式 x3+ax2+bx−5=0 が 虚数解x=1+2iをもつとき・・・ 次のようにしてa, bの値が定まり,残りの解も求まります。
○ 虚数x=1+2iが解であるとき,
(1+2i)3+a(1+2i)2+b(1+2i)−5=0から (a, bの式1)+(a, bの式2)i=0・・・(A) のように変形すると, a, bが実数であるから
※ポイントは(A)の式が、実部と虚部の2つの式に分けられるところにあります:
□,○が実数のとき □+○i = 0 ならば □=0 かつ○=0
○ 実数x=1などが解であるような場合,
13+a×12+b×1−5=0からは a+b−4=0となり, 未知数が2つで方程式が1つのため,a, bが定まりません。 |
【例題】
a, bは実数の定数とする。3次方程式 x3+ ax2 + bx − 5 = 0 が 虚数解 x = 1 + 2i をもつとき,定数a, bの値を求めよ。また,他の解を求めよ。 (答案) x= 1 + 2i が解であるから, (1+ 2i )3 + a(1 + 2i )2 + b(1 + 2i ) − 5 = 0 これを整理すると,
1+3×2i+3(2i)2+(2i)3
+a(1+4i+4i2) +b(1+2i) −5=0 (1+6i−12−8i)+a(−3+4i)+b(1+2i)−5=0 (−11−2i)+a(−3+4i)+b(1+2i)−5=0 (−3a+b−6)+(4a+2b−2)i=0 4a+2b−2= 0 ・・・(2) これより, a=−3,b=7 ・・・(答) また,x3− 3x2 + 7x − 5 = 0 を因数定理を用いて解くと
|