|
xとyの式で表わされました。 例 y = 2x + 3 このページで説明する媒介変数表示とは,x座標とy座標を他の変数の関数として表わしたものをい います。 x = t2 - 3
|
|
xとyの式で表わされました。 例 y = 2x + 3 このページで説明する媒介変数表示とは,x座標とy座標を他の変数の関数として表わしたものをい います。 x = t2 - 3
|
|
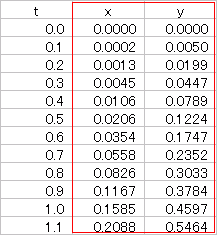
■ 媒介変数表示のイメージ 例1 物理の公式を用いると,高さ10(m)の屋上から水平方向に4(m/秒)の速さで投げ出された物体のt秒後のx座標とy座標は次の式で表わされます。 x = 4t※ t の値の上にマウスを置くと,対応するx,yの値とグラフ上の点の位置が 示されます。 この例では,時刻 t を媒介変数としてx座標とy座標が決まり,
|
|
■ 例2
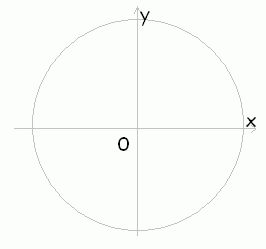
右の表は,動径がx軸の正の向きとなす角をθ(度)としたとき, x = cosθで与えられる点x,yの座標で,グラフはこれを点で示したものです。 この場合,x,yは角度θによる媒介変数表示で表わされ,グラフは原点を中心とする半径1の円になります。 ※ θ の値の上にマウスを置くと,対応するx,yの値とグラフ上の点の位置が示されます。
|
|
|
■ 媒介変数の消去とは -- 媒介変数表示をx,yの関係式に直すには,媒介変数を消去します。それはなぜ? 例 次の媒介変数表示において,tがすべての実数を変化するとき,点x,yの通るグラフの方程式をx,yの関係式で表わすことを考えると: x = 2t + 1・・・(1)(1)(2)は,次の式と同じ ※ 上の□枠内において,共通の t が2つの表現で結ばれているのが第1のポイントです。 ※ 次にt が舞台から消えるのが第2のポイントです。 すなわち,x,yの関係式は 3(x - 1) = 2(y + 1) |
| t:必要ならばいつでも登場できるが,当面舞台から隠れる
xとy:つながっている 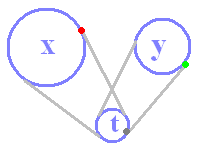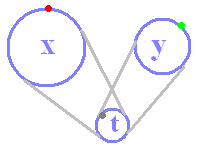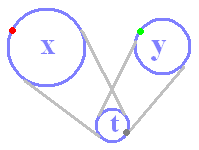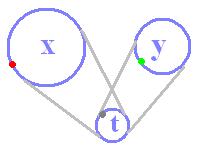
 |
■ 要点 --媒介変数の消去 (x,y関係式; 軌跡の方程式の求め方)
○1
□2
●3
■4
※
 |
|
例○1 次の媒介変数表示をx,yの関係式に直しなさい。
x = -t +3・・(1)例□2 次の曲線の方程式を,yをxの関数として表わしなさい。 x = t - 1・・(1)例●3 次の式で表わされる点(x,y)が動く軌跡の方程式を求めなさい。 x = √t・・(1)例■4 実数 t が変化するとき,次の点(x,y)がどのような曲線上を動くか述べなさい。 x = cost・・(1)例※ 次の媒介変数表で表わされる曲線(サイクロイド)は,媒介変数の消去によるx,y関係式に簡単にはできません。 x = t - sintExcelのグラフで散布図を選択すると次のような概形が描けます。 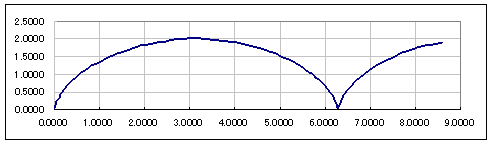 |
|
■ 問題 1 次の媒介変数表示で表わされる曲線の方程式を右の選択肢から選びなさい。 |
| [選択肢] |
[ヒント]
 |
[参考]
 |
| 2 次の媒介変数表示で表わされる曲線の方程式を右の選択肢から選びなさい。
|
| [選択肢] |
[ヒント]
 |
[参考]
 |
(む)3 次の媒介変数表示で表わされる曲線の方程式を右の選択肢から選びなさい。
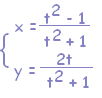 |
| [選択肢] |
[ヒント]
 |
[参考]
 |
4 t が全実数を変化するとき,次の2直線の交点の軌跡の方程式を求めなさい。
tx - y - t = 0 ・・・(1) |
| [選択肢] |
[ヒント]
 |
[参考]
 |
|
[注]直前にPC版から入られた場合は,自動転送でスマホ版に来ていますので,ブラウザの[戻るキー]では戻れません(堂々巡りになる).下記のリンクを使ってメニューに戻ってください.
|
|
■[個別の頁からの質問に対する回答][媒介変数表示について/16.12.12]
媒介変数表示の例2の345度の時に表示する点が間違えているかもしれません
とてもわかりやすかったです、復習に使わせていただきました
■[個別の頁からの質問に対する回答][媒介変数表示について/16.11.14]
=>[作者]:連絡ありがとう.ブラウザによっては表中の座標のマイナスの符号が上下にずれるものがありましたので訂正しました.また,ブラウザによっては点が縦方向に微妙に下にずれる場合がありましたので訂正しました. とてもわかりやすかったです!
ありがとうございます
役に立ちました!
大学の過去問などから引用した問題なども掲載してもらえるとありがたいです
=>[作者]:連絡ありがとう. |