ｔ　が変化すれば，ｘが変化し，ｙも変化するので，
ｘ　と　ｙ　が連動しているように見えます。

実際，ｘが決まればｙが決まります。

x = 4t
y = -4.9t² + 10

　この例では，時刻　t　を媒介変数としてｘ座標とｙ座標が決まり，
それぞれの　ｔ　の値について点が定まります。

x = cosθ
y = sinθ

　この場合，x,yは角度θによる媒介変数表示で表わされ，グラフは原点を中心とする半径１の円になります。 

※　θ　の値の上にマウスを置くと，対応するｘ，ｙの値とグラフ上の点の位置が示されます。　 

x = 2t + 1・・・(1)
y = 3t - 1・・・(2)

---

3(x - 1) = 2(y + 1)
あるいは
3x - 2y - 5 = 0　・・・答

※　左の□枠内において，共通の ｔ が２つの表現で結ばれているのが第１のポイントです。

※　次にｔ が舞台から消えるのが第２のポイントです。

○１
　上の例のように，２つの式をｔ について明示的に解いて，これらが等しいことから，ｘ，ｙの関係式を求められる場合があります。

□２
　２つの式から t を明示的に解くことができなくても，１つの式から　t =・・・　の形に直し，もう一方の式に代入することによりｔ を消去してｘ，ｙの関係式が求められる場合があります。

●３
　t　を代入消去するときに，媒介変数に付着していた条件は，ｘやｙの条件として引き継がなければならないことがあります。

■４
　一旦 t= という形に解くことは重要でなく，ただ単に t が消去できればよいので，ｘ，ｙの式をよく観察して関係式を作ります。

※
　媒介変数が簡単には消去できないものもあります。
ア　このようなものにおいては，曲線の方程式は媒介変数表示でのみ表わされます。
イ　曲線の概形が必要なときは，幾つかのｔの値を元に，点をプロットすれば分かります。
　表計算ソフトExcelで次の赤枠部分を選択してから，グラフ→散布図などとします。

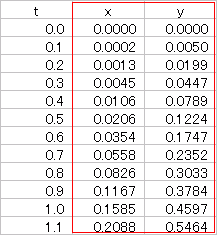
x = -t +3・・(1)
y = 2t + 1・・(2)
(t は全実数)・・(3)

---

(1)より t = 3 - x
これを(2)に代入
y = 2(3 - x) + 1= -2x +7　・・・答・・(4)
(なお，(3)よりｘも全実数となり(4)の直線の全部が答。
数学では「制限のあるものは言わなければならない」が，「制限のないものは，何も言わなくてよい」ので
単に　y = -2x +7　を答とすればよい。)

x = t - 1・・(1)
y = 2t² + 3・・(2)
(数学では「制限のあるものは言わなければならない」が，「制限のないものは，何も言わなくてよい」ので，特に記述がなければ，ｔ は全実数：制限がないものとして扱う)・・(3)

---

(1)より t = x + 1
これを(2)に代入すると
y =2(x + 1)² + 3・・答・・(4)
(t は全実数で，(1)よりｘは全実数：何も言わなくてよい。)

x = √t・・(1)
y = 3t + 1・・(2)

---

(1)より x =√t ≧ 0
[ｔ は消える　→　条件はｘが引き継ぐ：ｘ≧0］
(1)よりt = x²　を(2)に代入
y = 3x² + 1 (ｘ≧0)・・・答

x = cost・・(1)
y = sint・・(2)

---

sin²t + cos²t = 1はどんなｔについても成立するから
x² + y² = 1・・答・・(3)
(実際には，(1)(2)において-1≦cost≦1，-1≦sint≦1だから-1≦x≦1，-1≦y≦1であるが，(3)を満たすｘ，ｙはこの制限を満たしているので，定義域について何も言わなくてよい。)

x = t - sint
y = 1 - cost

tx - y - t = 0　・・・(1)
x + ty + 1 = 0 ・・・(2)