|
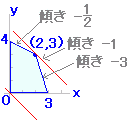
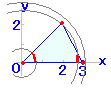
○ 図1のように,連立不等式 x≧0 , y≧0 , y≦−x+2 で表わされる三角形の領域において,y−x の取りうる値の範囲を求めたいものとする.
図1
○ y−x のままでは,単なる「式」で x も y も変るので分かりにくい.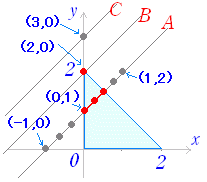 これを,y−x=k すなわち y=x+k とおくと「方程式」になり「直線」を表わす. このように,求めたい式の値を … =k とおき,k の取り得る値の範囲を考えると「図形」に対応させて考えることができる. ■ 1つの直線上では k の値は同じ ○ 例えば,図1のAの直線の方程式は y=x+1 で,k=1 になっている. この直線の方程式が y=x+1 だということは,この直線上のどの点でも y=x+1 すなわち y−x=1 が成り立つことを表わしている. x=−1, y=0 の点では,0−(−1)=1○ 図1のBの直線の方程式は y=x+2 で,この直線上のどの点でも y−x の値は 2 になる. x=0, y=2 の点では,2−0=2○ 連立不等式 x≧0 , y≧0 , y≦−x+2 で表わされる領域は,上の水色の三角形の内部及び周上であるが,この領域内における y−x の最大値と最小値を求めるには次のように考えるとよい. y−x=k すなわち y=x+k とおくと,k は直線の切片を表わすから,上に行くほど大きく,下に行くほど小さくなる. 例えば,直線Cは y=x+3 で k の値は大きいが,この直線は与えられた三角形の領域を通っていない. |
|
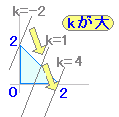
[考え方] ○与えられた領域をある直線が通っている⇔領域内でその直線の k の値がとれる. ▼与えられた領域をある直線が通っていない⇔領域内でその直線の k の値がとれない. 上の三角形の領域では, ▼k=3 の値はとれない. ○k=2 の値はとれる.(例えば点 (0, 2) において y−x=2 ) ○k=1 の値はとれる.(例えば点 (0, 1) において y−x=1 ) …… ○k=−2 の値はとれる.(例えば点 (0,−2) において y−x=−2 ) ▼k=−3 の値はとれない. このように, y=x+k とおいて k の値を変化させると,直線はエレベーターのように上下し,点 (0, 2) において最大値 2,点 (2, 0) において最小値 −2 となる. 上の問題では,ある直線 y=x+k が通っている点が1つでもあれば,その k の値は領域内でとれる値となり,通るべき点は2つも3つもいらないことに注意 実際には,最大値 k=2 となる点は (0, 2) の1点だけであり,最小値 k=−2 となる点は (2, 0) の1点だけであるが,これで十分 他方において,-2<k<2 となる点はそれぞれたくさんあるが,ある値がとれるかどうかという問題(最大値・最小値)にとっては,点が幾つあっても答は変らないので,「上の三角形の領域の内部」は最大値・最小値という問題に関係なく,三角形の周上だけで取りうる値はすべて実現されている. 一般に,求める式の形が y=x+k のように直線図形になっているときは,つねに周上で最大値・最小値をとることが知られている. |
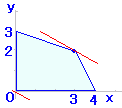
 (1) まず領域を図示する.
(1) まず領域を図示する.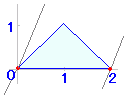
 [解答]
[解答]
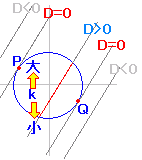 [解答]
[解答]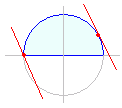
 [解答]
[解答]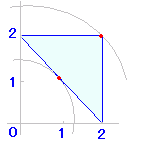
 [解答]
[解答]