→ 携帯版は別頁

x=aのときy=bという形の式

すなわち，F(a)=bという式

すなわち，１つの通る点(a, b)

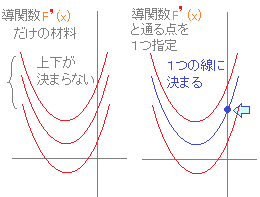【要点】
　一般に，導関数F'(x)だけが与えられたとき，元の関数F(x)の定数項Cは決まらない．
　導関数F'(x)と初期条件F(a)=bが与えられると，定数項Cが決まり，関数F(x)が確定する

○［次の条件を満たす関数F(x)は確定できます］
\( F'(x)=2x+1,\hspace{5px}F(0)=1 \)…(1)
×［次の条件を満たす関数F(x)は確定できません］
\( F'(x)=2x+1,\hspace{5px}F'(0)=1 \)…(2)

(1)では，\( F(x)=x^2 +x+C \)と初期条件F(0)=1からCが求められますが
(2)では\( F(x)=x^2 +x+C \)に対して，F'(0)=1は初期条件になっておらず，Cを求める手掛かりがありません．（F'(x)の式ばかりだと，１つもCが含まれていないので，Cを決めることができません）

《要点》
まず不定積分を求め，次にＣを定めます.

○はじめに左の式を一つクリックし，続けて答をクリックすると消えます．
○間違えば消えません．間違ったときは，解答欄を連打するのではなく，問題を選び直すことから始めてください．間違ったとき，[解説]ボタンが見えている間にそれを押せば，「左側の問題に対する解説」が出ます．
○[解説]を使って解説を読む場合でも，読まない場合でも，新しい問題を選べば解答を再開できます．

※暗算ではできません．計算用紙を使って答えてください．

F'(x)=1より
\( \displaystyle F(x)=\int 1 dx=x+C \)
次にF(0)=5よりC=5
結局F(x)=x+5 \( F'(x)=2x-1 \)より
\( \displaystyle F(x)=\int (2x-1) dx=x^2-x+C \)
次にF(1)=3よりC=3
結局\( F(x)=x^2-x +3 \) \( F'(x)=x^2+2x \)より
\( \displaystyle F(x)=\int (x^2 +2x) dx \)
\( =\dfrac{x^3}{3}+x^2+C \)
次にF(3)=0より18+C=0
C=−18
結局\( F(x)=\dfrac{x^3}{3}+x^2 -18 \) \( F'(x)=x^2+2x \)より
\( \displaystyle F(x)=\int (x^2+2x) dx \)
\( =\dfrac{x^3}{3} +x^2+C \)
次にF(0)=3よりC=3
結局\( F(x)=\dfrac{x^3}{3}+ x^2 +3 \) \( F'(x)=2x-1 \)より
\( \displaystyle F(x)=\int (2x-1) dx \)
\( =x^2-x+ C \)
次にF(3)=1より6+C=1
　C=−5
結局\( F(x)=x^2-x-5 \) \( F'(x)=x(x-1) \)より
\( \displaystyle F(x)=\int x(x-1) dx \)
\( \displaystyle =\int(x^2-x)dx=\dfrac{x^3}{3}-\dfrac{x^2}{2}+C \)
次にF(1)=0より\( -\dfrac{1}{6}+C=0 \)
\( C=\dfrac{1}{6} \)
結局\( F(x)=\dfrac{x^3}{3}-\dfrac{x^2}{2} +\dfrac{1}{6} \) \( F'(x)=3x^2-2x \)より
\( \displaystyle F(x)=\int (3x^2-2x) dx \)
\( =x^3-x^2 +C \)
次にF(−1)=1より−2+C=1
C=3
結局\( F(x)=x^3-x^2+3 \) \( F'(x)=3x^2-2x \)より
\( \displaystyle F(x)=\int (3x^2-2x) dx \)
\( =x^3-x^2 +C \)
次にF(1)=−1よりC=−1
結局\( F(x)=x^3-x^2-1 \) \( F'(x)=1 \)より
\( \displaystyle F(x)=\int 1 dx=x+C \)
次にF(5)=0より5+C=0
C=−5
結局F(x)=x−5 \( F'(x)=x(x^2-1) \)より
\( \displaystyle F(x)=\int x(x^2-1) dx \)
\( \displaystyle =\int(x^3-x)dx=\dfrac{x^4}{4}-\dfrac{x^2}{2} +C \)
次にF(1)=0より\( -\dfrac{1}{2} +C=0 \)
\( C=\dfrac{1}{4} \)
結局\( F(x)=\dfrac{x^4}{4}-\dfrac{x^2}{2} +\dfrac{1}{4} \)