|
← PC用は別頁
しかし,円周の長さ,円の面積など長さや面積を角度で表わすためには, θ=(弧の長さ)÷(半径の長さ) で定義される弧度法(単位はラジアン)の方が有利で,特に微分積分では角度の単位としては弧度法を使います。
度数法(60分法) ・・・ 単位は度 弧度法 ・・・単位はラジアン(省略するのが普通) |
|
(参考) 弧度法の単位:ラジアンはなぜ省略できるか。
○同じもので割ると長さの単位などが約分で消えます。
|
|
← PC用は別頁
しかし,円周の長さ,円の面積など長さや面積を角度で表わすためには, θ=(弧の長さ)÷(半径の長さ) で定義される弧度法(単位はラジアン)の方が有利で,特に微分積分では角度の単位としては弧度法を使います。
度数法(60分法) ・・・ 単位は度 弧度法 ・・・単位はラジアン(省略するのが普通) |
|
(参考) 弧度法の単位:ラジアンはなぜ省略できるか。
○同じもので割ると長さの単位などが約分で消えます。
|
|
○ 度をラジアンに直すには
度の単位で表された角度θ°を,ラジアンの単位に直すには, 180°=π(ラジアン) を使って比例で考えるとよい.
180:θ=π:x …(1)
結果を公式にして覚えたい人は,180x=πθをxについて解いて,次の(2)で覚えてもよい. |
||||||||||||||||||||||||||||||||||||||||
|
例
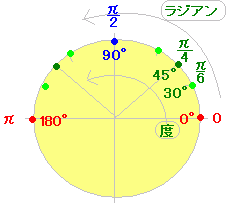 ※実際には,よく登場する角度は30°,45°の整数倍ばかりなので,個別に計算するよりも,上の図に出てくる角度を2倍,3倍,...とする方が早い.
|
|
【問題】 等しいものを選びなさい。 (初めに度数法の角度をクリックし,続いて弧度法で表わした角度をクリックしなさい。合っていれば消えます。間違えば消えません。) 度数法
弧度法
 |
|
|
|
■[個別の頁からの質問に対する回答][弧度法の単位ラジアンについて/17.2.24]
数学はさっぱり駄目な文系大卒の32歳です。
現在業務の都合から電験三種の勉強をしていますが、電験用の基礎数学の参考書ですら理解に苦しみ、ネットを徘徊しているときに出会いました。
非常にわかりやすく解説して頂き、何とか参考書を読み解くことができるようになりました。
■[個別の頁からの質問に対する回答][弧度法の単位ラジアンについて/17.2.21]
=>[作者]:連絡ありがとう. わかりやすいです。
問題があるのがすばらしいです。
ありがとうございます。
=>[作者]:連絡ありがとう. |