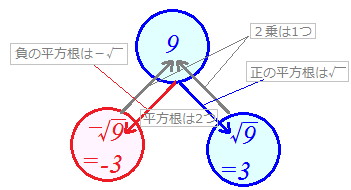
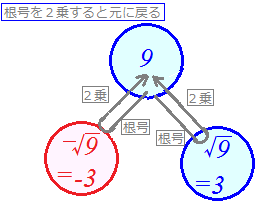
■平方根のうちで整数や分数には直せないもの
02=0 , 12=1 , 22=4 , 32=9 , 42=16 , 52=25 , ...だから
 \( \displaystyle \sqrt{0} \)=0 \( \displaystyle \sqrt{0} \)=0
 \( \displaystyle \sqrt{1} \)=1 \( \displaystyle \sqrt{1} \)=1
 \( \displaystyle \sqrt{4} \)=2 \( \displaystyle \sqrt{4} \)=2
 \( \displaystyle \sqrt{9} \)=3 \( \displaystyle \sqrt{9} \)=3
 \( \displaystyle \sqrt{16} \)=4 \( \displaystyle \sqrt{16} \)=4
 \( \displaystyle \sqrt{25} \)=5, ... \( \displaystyle \sqrt{25} \)=5, ...です.
根号の中を先に決めて,  \( \displaystyle \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{10},.. \) \( \displaystyle \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{10},.. \)のような数字を考えると,これらは整数や分数では表せないことが知られています.
1つの例として,  \( \displaystyle \sqrt{2} \) \( \displaystyle \sqrt{2} \)はどんな数字になるか調べてみると,これは a2=2となるような正の数 aを表しています.
1.42=1.96←小さ過ぎる
1.52=2.25←大き過ぎる
1.452=2.1025←大き過ぎる
1.412=1.9881←小さ過ぎる
1.422=2.0164←大き過ぎる
1.414213562=1.9999999932...←小さ過ぎる
1.414213572=2.0000000215...←大き過ぎる
このようにして,  \( \displaystyle \sqrt{2} \)=1.41421356...辺り \( \displaystyle \sqrt{2} \)=1.41421356...辺りの数字になりますが,この小数はどこまで行っても終わりません.
近似値としては,  \( \displaystyle \sqrt{2} \)≒1.41 \( \displaystyle \sqrt{2} \)≒1.41を使うことが多いですが,正確な値で表したいときは根号を付けたまま
 \( \displaystyle \sqrt{2} \) \( \displaystyle \sqrt{2} \)
で表します.
 \( \displaystyle \sqrt{3},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{10},.. \) \( \displaystyle \sqrt{3},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{10},.. \)なども同様にして,根号の中が「平方数(=整数の2乗)」になっていなければ簡単な整数にならないので,根号をつけたままで表します.
(昔の覚え方)…今の生徒は3桁まで言えれば十分
=1.41421356... 一夜一夜に人見頃(ひとよひとよにひとみごろ)
夜桜見物で,一夜ごとに花が見頃になっていくに連れて,人の数も見頃になっていく情景を描いたものか・・・
=1.7320508... 人並みにおごれや(ひとなみにおごれや)
=2.2360679... 富士山麓オーム鳴く(ふじさんろくオームなく)
=2.44949... 似よ良く良く(によよくよく),二夜シクシク(ふたよしくしく)
[前の方]双子の兄弟の話かも・・・[後の方]泣き続けた・・・
=2.64575... [菜]に虫いない(なにむしいない)
語呂合わせの都合で,先頭の7も読んでしまう.・・・
※ =1, =2, =2, =3は,覚える必要なし.
|
【例題】
(解答)
 \( \displaystyle \sqrt{9}\lt \sqrt{10} \lt \sqrt{16} \)だから \( \displaystyle \sqrt{9}\lt \sqrt{10} \lt \sqrt{16} \)だから \( \displaystyle 3\lt \sqrt{10} \lt 4 \)が成り立つ…(答) \( \displaystyle 3\lt \sqrt{10} \lt 4 \)が成り立つ…(答)
(詳しく書けば \( \displaystyle \sqrt{10}=3.16227... \)になります.) \( \displaystyle \sqrt{10}=3.16227... \)になります.)
【問題3】
(1)  \( \displaystyle \sqrt{12} \) \( \displaystyle \sqrt{12} \)の値について,正しいものを選んでください.
 \( \displaystyle 1\lt \sqrt{12} \lt 2 \) \( \displaystyle 1\lt \sqrt{12} \lt 2 \)
 \( \displaystyle 2\lt \sqrt{12} \lt 3 \) \( \displaystyle 2\lt \sqrt{12} \lt 3 \)
 \( \displaystyle 3\lt \sqrt{12} \lt 4 \) \( \displaystyle 3\lt \sqrt{12} \lt 4 \)
 \( \displaystyle 100 \lt \sqrt{12} \lt 121 \) \( \displaystyle 100 \lt \sqrt{12} \lt 121 \)
 \( \displaystyle 121 \lt \sqrt{12} \lt 169 \) \( \displaystyle 121 \lt \sqrt{12} \lt 169 \)
解説
 \( \displaystyle \sqrt{9}\lt \sqrt{12} \lt \sqrt{16} \)だから \( \displaystyle \sqrt{9}\lt \sqrt{12} \lt \sqrt{16} \)だから \( \displaystyle 3\lt \sqrt{12} \lt 4 \) \( \displaystyle 3\lt \sqrt{12} \lt 4 \)
(詳しく書けば \( \displaystyle \sqrt{12}=3.46410... \)になります.) \( \displaystyle \sqrt{12}=3.46410... \)になります.)
(2)  \( \displaystyle \sqrt{7} \) \( \displaystyle \sqrt{7} \)の値について,正しいものを選んでください.
 \( \displaystyle 1\lt \sqrt{7} \lt 2 \) \( \displaystyle 1\lt \sqrt{7} \lt 2 \)
 \( \displaystyle 2\lt \sqrt{7} \lt 3 \) \( \displaystyle 2\lt \sqrt{7} \lt 3 \)
 \( \displaystyle 3\lt \sqrt{7} \lt 4 \) \( \displaystyle 3\lt \sqrt{7} \lt 4 \)
 \( \displaystyle 13 \lt \sqrt{7} \lt 15 \) \( \displaystyle 13 \lt \sqrt{7} \lt 15 \)
 \( \displaystyle 48 \lt \sqrt{7} \lt 50 \) \( \displaystyle 48 \lt \sqrt{7} \lt 50 \)
解説
 \( \displaystyle \sqrt{4}\lt \sqrt{7} \lt \sqrt{9} \)だから \( \displaystyle \sqrt{4}\lt \sqrt{7} \lt \sqrt{9} \)だから \( \displaystyle 2\lt \sqrt{7} \lt 3 \) \( \displaystyle 2\lt \sqrt{7} \lt 3 \)
(詳しく書けば \( \displaystyle \sqrt{7}=2.64575... \)になります.) \( \displaystyle \sqrt{7}=2.64575... \)になります.)
(3)  \( \displaystyle \sqrt{30} \) \( \displaystyle \sqrt{30} \)の値について,正しいものを選んでください.
 \( \displaystyle 3\lt \sqrt{30} \lt 4 \) \( \displaystyle 3\lt \sqrt{30} \lt 4 \)
 \( \displaystyle 4\lt \sqrt{30} \lt 5 \) \( \displaystyle 4\lt \sqrt{30} \lt 5 \)
 \( \displaystyle 5\lt \sqrt{30} \lt 6 \) \( \displaystyle 5\lt \sqrt{30} \lt 6 \)
 \( \displaystyle 6 \lt \sqrt{30} \lt 7 \) \( \displaystyle 6 \lt \sqrt{30} \lt 7 \)
 \( \displaystyle 8 \lt \sqrt{30} \lt 9 \) \( \displaystyle 8 \lt \sqrt{30} \lt 9 \)
解説
 \( \displaystyle \sqrt{25}\lt \sqrt{30} \lt \sqrt{36} \)だから \( \displaystyle \sqrt{25}\lt \sqrt{30} \lt \sqrt{36} \)だから \( \displaystyle 5\lt \sqrt{30} \lt 6 \) \( \displaystyle 5\lt \sqrt{30} \lt 6 \)
(詳しく書けば \( \displaystyle \sqrt{30}=5.47722... \)になります.) \( \displaystyle \sqrt{30}=5.47722... \)になります.)
|