|
【グラム・シュミットの直交化法】 n個の1次独立なベクトル とおく.このとき, 次に,ベクトル 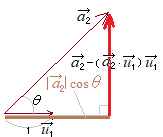
は が このとき を作ると, とおくと, |
同様にして を作ると, とおくと, とおくと, |
|
【グラム・シュミットの直交化法】 n個の1次独立なベクトル とおく.このとき, 次に,ベクトル 
は が このとき を作ると, とおくと, |
同様にして を作ると, とおくと, とおくと, |
|
【例題1】
(解答)グラム・シュミットの直交化法を用いて,次のベクトルから正規直交系を作ってください. とおく. 次に, ここで, したがって (注意) 1組の1次独立なベクトルから,グラム・シュミットの直交化法によって,正規直交系がただ1通りに決まる訳ではない. 処理するベクトルの並べ方(順序)によって,結果として作られる正規直交系は変わる. 例えば,上記の問題を |
【問題1】
解答を見る解答を隠すグラム・シュミットの直交化法を用いて,次のベクトルから正規直交系を作ってください.
(解答)
とおく. 次に, ここで, とおく さらに とおく.ここに, |
|
※グラム・シュミットの直交化法により,n次元空間のn個の1次独立なベクトル
【例題2】
(解答)次のベクトルで生成される,R4の部分空間の正規直交基底を求めよ. (b) (1, 2, 1, 0)と(1, 2, 3, 1) (「ラング線形代数学(上)」芹沢正三訳/ちくま学芸文庫
P.223からの引用) 次に, とおくと, ここで |
【問題2】
解答を見る解答を隠す次のベクトルで生成される,R3の部分空間の正規直交基底を求めよ. (b) (1, 1, −1)と(1, 0, 1) (「ラング線形代数学(上)」芹沢正三訳/ちくま学芸文庫
P.222からの引用)
(解答)
次に, とおくと, ここで |
|
【例題3】
(解答)区間[0, 1]の上の連続実関数のなすベクトル空間を考える.このような2つの関数 で定義する. (「ラング線形代数学(上)」芹沢正三訳/ちくま学芸文庫
P.223からの引用) であるから, |
次に, だから ここで であるから, |
|
【問題3.1】
解答を見る解答を隠す区間[0, 1]の上の連続実関数のなすベクトル空間を考える.このような2つの関数 で定義する. (「ラング線形代数学(上)」芹沢正三訳/ちくま学芸文庫
P.223からの引用)
(解答)
さらに, (参考) 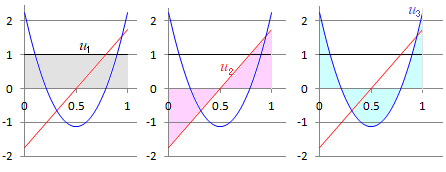 が成り立つ.(これは定数 |
関数の正規直交化においてスカラー積を定義する区間は,脇役や添え物ではない.上記の【問題3.1】と同じ関数を使っても,区間を変えると結果は全く別のものになる.
【問題3.2】
解答を見る解答を隠す区間[−1, 1]の上の連続実関数のなすベクトル空間を考える.このような2つの関数 で定義する.
(解答)
計算はほぼ同様に行えばよい.積分の区間だけは−1~1とすればよい. この問題では,逆に上記の関数が正規直交系になっていることを示す検算を行ってみる. ≪直交系であることの証明≫ は,奇関数を[−1, 1]で積分するものだから0である. は,奇関数を[−1, 1]で積分するものだから0である. 以上により,区間[−1, 1]において関数 ≪正規系であることの証明≫ 以上により,区間[−1, 1]において関数 (参考) 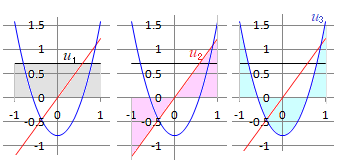 が成り立つ.(これは定数 |
| ■このサイト内のGoogle検索■ |