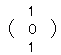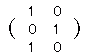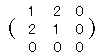|
■行列の相等,和,差,実数倍 [解説] ●行列の相等 ・2つの行列A,Bの型が一致し,かつ,対応する成分が各々等しいとき,AとBは等しいといい,A=Bと書きます。 ・ |
等しくない例
型が一致しない。 A= |
| [問題] |
 |
| [解説]
●行列の和 ・2つの行列の型が一致するとき,行列の和を次のように定義します。 2×2行列での例 A+B= ・2つの行列の型が一致するとき,行列の差を次のように定義します。 2×2行列での例 A-B= ●行列の実数倍 ・行列のt倍は,各成分をt倍した行列とします。 2×2行列での例 |
3個以上の行列の和は,2つずつの和の繰り返し適用で定義します。
(A+B)+C または A+(B+C) ((A+B)+C)+D 、A+(B+(C+D))・・・など ここで,行列の和については |
| [問題] |
 |
| 2 |

|
| ●零行列
成分がすべて0である行列を零行列といいます.行列の型が分かっているとき,零行列は単に0で表します。
1×2型の零行列
2×2型の零行列 2×3型の零行列 型が同じとき,A+0=0+A=Aが成立します.
例えば,2×2行列では
が成り立つことは明らかでしょう 任意の行列Aについて0A=0,任意の実数tについてt0=0が成立します.
例えば,2×2行列では
が成り立つことは明らかでしょう |
●行列の和の性質
※ 行列で割ることはできませんが,行列の和,差、実数倍,展開などが自由にできるので,次のような行列の方程式も解けます。
また,次のような連立方程式でも { (1)+(2) }÷2や{ (1)−(2) }÷2のような変形は,行列の和,差、実数倍でできるので,普通の連立方程式と同じように解くことができます. ※行列で割ることはできません. 例えば,左辺が2つの行列の積 とすることはできません. 詳しくは,行列の積を学ぶと分かりますが,一般に行列の積は |
|
[問題]
3 |

|
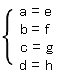
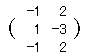 との和が定義できるものを選びなさい。
との和が定義できるものを選びなさい。