|
○右図1のような立体[分かりやすくするために階段状に表示しているが,実際は滑らかな局面で囲まれているものとする]の体積(縦棒の体積の総和)は,面積要素ds=dxdyに高さz=f(x, y)を掛けて得られる体積要素
dV=f(x, y)ds=f(x, y)dxdy の総和として,定義域D上の重積分 f(x, y)dxdy で求めることができます.
図1
○f(x, y)が連続関数で,各変数の定義域がa≦x≦b, α≦y≦βであるとき,この重積分は
  f(x, y)dx f(x, y)dx 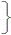 dy…(1) dy…(1)または  f(x, y)dy f(x, y)dy 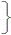 dx…(2) dx…(2)のように,1変数の積分の繰り返しによって行うことができます. (1)は右図2のように,まず変数yを固定して,各々のyについて,xで積分し(図で示した壁の面積S(y)を求めて),次にyの関数として表されたその面積をyで積分することによって体積を求めることに対応しています.
図2
(2)は図3のように,初めにxを固定してyで積分し,図で示した壁の面積S(x)を求めて,次にxで積分するものです.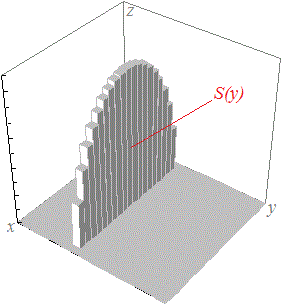
図3
 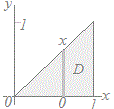 ○変数の定義域が0≦x≦1, 0≦y≦xのように他の変数に依存しているときは
○変数の定義域が0≦x≦1, 0≦y≦xのように他の変数に依存しているときは
 f(x, y)dy f(x, y)dy  dx dx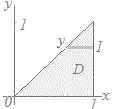 または0≦y≦1, y≦x≦1として
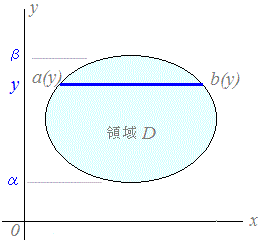
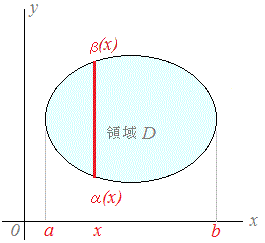
または0≦y≦1, y≦x≦1として f(x, y)dx f(x, y)dx  dy dyのように計算できます. 一般に,図4(その平面図が図5)のように積分領域Dの境界線が長方形でなく,変数x, yの値に依存している場合  f(x, y)dx f(x, y)dx  dy…(A) dy…(A)のように,固定された変数yの値に依存する積分区間 a(y)≦x≦b(y)についてxで積分し,できた面積S(y)(これはyの関数になる)を積分区間α≦y≦βについてyで積分します.
図4
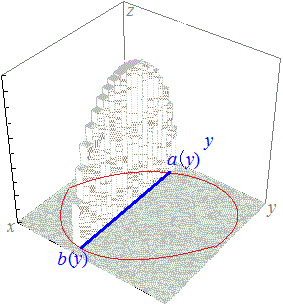
図5
もしくは
  f(x, y)dy f(x, y)dy  dx…(B) dx…(B)のように,固定された変数xの値に依存する積分区間 α(x)≦y≦β(x)についてyで積分し,できた面積S(x)(これはxの関数になる)を積分区間a≦x≦bについてxで積分します.
図6
 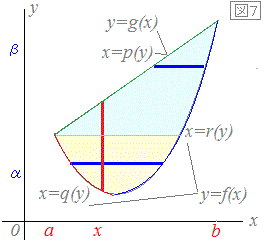 ※ 理論上は,(A)と(B)のどちらでも求められますが,実際の計算の複雑さは大いに違う場合があります.
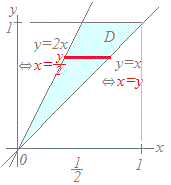
※ 理論上は,(A)と(B)のどちらでも求められますが,実際の計算の複雑さは大いに違う場合があります.図7の場合は,初めに縦に切る(赤線)と(先にyで積分すると)積分区間の下端と上端は場合分けの必要がなく1組で済みますが,初めに横に切る(青線)と(先にxで積分すると)積分区間の下端と上端は,図の水色の領域の場合と黄色の場合とで,積分区間の組合せが異なってきます. |

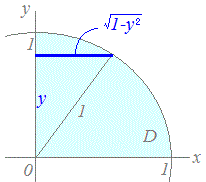 積分の領域
積分の領域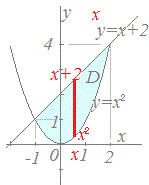 右図のようなグラフになり,
右図のようなグラフになり,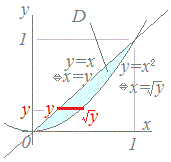 右図のようなグラフになり,
右図のようなグラフになり,