|
■文字係数方程式の解
ｘの方程式 ａｘ＝ｂ の解は (1) ａ≠0のとき， i) b=0 のとき，（0x=0の形だから） |
例
ｘについての方程式 (ｋ2-1)ｘ＝ｋ-1 の解は， ア) ｋ≠±1 のとき ｘ＝ 
イ） ｋ＝1のとき 0x=0 となり，ｘは任意の実数。 ウ） ｋ＝－１のとき 0ｘ＝-2 となり，解なし。 |
|
■定数項が0である連立方程式が原点以外の解を持つ条件
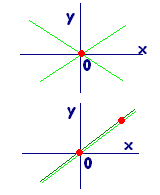
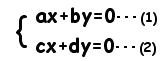  原点 x=y=0は(1)(2)の解となるのは，当然のこと，自明のことです。 （代入すれば分かります。） ｘ＝ｙ＝0を連立方程式(1)(2)の自明解といいます。 次に，連立方程式(1)(2)が，自明解以外の解(自明でない解)を持つ条件を考えます。 原点を通る２つの直線が，原点以外の点でも「交わっている」ことは考えにくいことですが，右図のように，「２直線が一致する場合」に限り原点以外の点(x､y)で方程式が成立することとなります。 (1)(2)はΔ＝ad-bc=0のとき，平行かつ一致する２直線となります。 このとき，共有点は単に２個あるのでなく，直線上の点全部が共有点となります。 |
|
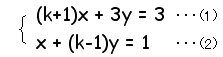を解きなさい。
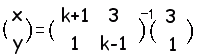より，
=
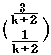・・・答
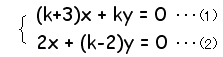が，ｘ＝ｙ＝0以外の解を持つように定数ｋの値を定めなさい。
..高卒～大学数学のメニューに戻る
●===メニューに戻る