最大角，最小角

...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ 高卒・大学初年度
*** 単元 ***
数と式不等式二次関数二次不等式三角比三角比と図形集合・命題・証明順列・組合せ確率整数の性質

※高校数学Ⅰの「三角比と図形」（正弦定理，余弦定理など）について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

↓正弦定理（解説）
↓正弦定理（問題）
↓分数型の方程式

↓余弦定理（解説）
↓三辺→角
↓余弦定理の2次方程式

↓筆算だけで解く問題(1)
↓筆算だけで解く問題(2)
↓最大角・最小角

↓ヘロンの公式
↓内接円の半径

↓形状問題
↓証明問題

↓三角形を解く
↓センター問題(1)
↓センター問題(2)
センター問題(3)

== 最大角，最小角 ==

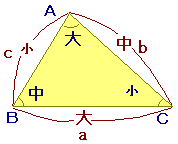
《解説》
■右図のような△ＡＢＣにおいて，

a≧b≧cならばA≧B≧C

です.
（逆も成り立ちます.）

つまり，

「対辺が長い」ならば「角度が大きい」
（「角度が大きい」ならば「対辺が長い」）

といえます.・・・(1)

(証明)・・余弦定理による証明・・・論理は簡単，変形はやや複雑
(方針)ａ≦ｂ←→cosＡ≧cosB←→A≦Bを示す.
cosＡ-cosB

＝｛a(b²+c²-a²)-b(a²+c²-b²)｝
＝｛c²(a-b)+a(b²-a²)-b(a²-b²)｝
＝｛c²(a-b)-(a²-b²)(a+b)｝
＝｛c²(a-b)-(a-b)(a+b)²｝
＝(a-b)(c²-(a+b)²)
＝(a-b)(c-a-b)(c+a+b)
ここで，ａ，ｂ，ｃ＞0だからｃ＋ａ＋ｂ＞0
また，三角形の成立条件によりｃ＜ａ＋ｂだからc-a-b<0
ゆえに，ａ≦ｂ←→cosＡ≧cosB←→Ａ≦Ｂ

(別の証明)・・正弦定理による証明・・論理は複雑，変形は少ない
(方針)ａ≦ｂ←→sinＡ≦sinB←→A≦Bを示す.
正弦定理により，ａ＝２ＲｓｉｎＡ，ｂ＝２ＲｓｉｎＢだから
ａ≦ｂ←→sinＡ≦ｓｉｎＢが言える.
０°＜Ａ,Ｂ＜180°においてsinＡ≦ｓｉｎＢとなる組合せは次の通り.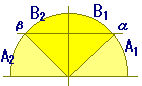

1)　A₁	B₁	→　Ａ≦Ｂ
2)　A₁	B₂	→　Ａ≦Ｂ
3)　A₂	B₁	*→(1)によりこのような三角形はない**
4)　A₂	B₂	*→(2)によりこのような三角形はない**

(*1)Ａ₂≧β，Ｂ₁≧αだからＡ₂+Ｂ₁≧α+β＝180°
　となり矛盾
(*2)Ａ₂+Ｂ₂≧90°+90°＝180°となり矛盾
1)2)よりＡ≦Ｂ

　△ＡＢＣにおいてＡ，Ｂ，Ｃのうち最も大ききな角度を最大角，最も小さな角を最小角と呼ぶと，上の図においては最大角はＡで最小角はＣです.
　(1)の関係から，最大角，最小角とその対辺の長さについて次のように言えます.

三角形において，最大角には最大辺が対応する.

三角形において，最小角には最小辺が対応する.

例
　三角形の３辺の長さが，７，８，１３　のとき，この三角形の最大角を求めなさい.
（答案）
　辺の長さ13が最も長いから，13に対応する角を求める.
　cosθ＝(7²+8²-13²)/(2・7・8)＝-1/2
　θ＝120°・・・(答)

《問題1》　　三角形の３辺の長さが，次のように与えられているとき，この三角形の最大角を求めなさい.
(1) 　１７，１５，８	30° 45° 60° 90° 120° 135° 150°

(2) 　５，１６，１９	30° 45° 60° 90° 120° 135° 150°

(3) 　３５，４３，１３	30° 45° 60° 90° 120° 135° 150°

(4) 　 $1$ ， $\sqrt{2}$ ， $\sqrt{5}$	30° 45° 60° 90° 120° 135° 150°

《問題２》　　三角形の３辺の長さが，次のように与えられているとき，この三角形の最小角を求めなさい.
(1) 　 $3 \sqrt{3}$ ， $\sqrt{7}$ ， $4$	30° 45° 60° 90° 120° 135° 150°

(2) 　 $3 + \sqrt{3}$ , $2 \sqrt{3}$ , $3 \sqrt{2}$	30° 45° 60° 90° 120° 135° 150°

《解説》
　筆算で角度まで求められるのは，30°または45°の整数倍の角度に限られますが，cosθの値まででよいときはそのような制限はなくなります.
例
　　三角形の３辺の長さが，次のように与えられているとき，この三角形について最大角の余弦を求めなさい.
　　ａ＝９，ｂ＝８，ｃ＝７
(答案)
　ａが最大なので，Ａが最大
　cosＡ＝（８²+7²-９²）/（２・８・７）＝2/7・・・（答）

《問題３》 1 　△ＡＢＣにおいて，sinＡ：sinＢ：sinC＝５：６：７とする.最大角をθとするとき，cosθ＝［　　］である. （日本工大入試問題からの引用）	左の空欄を埋めると， $\frac{1}{3}$ $\frac{2}{3}$ $\frac{1}{5}$ $\frac{2}{5}$ $\frac{3}{5}$ $\frac{4}{5}$

2 　三角形の３つの高さを各々４，９，６とするとき，最小角の余弦は.	左の空欄を埋めると， $\frac{5}{13}$ $\frac{14}{27}$ $\frac{29}{54}$ $\frac{101}{108}$

3 　△ＡＢＣの３辺がＢＣ＝ｘ²-ｘ+1，ＣＡ＝x²-2x，AB=2ｘ-1で表されている. (1)　３つの辺の大小関係を調べよ. (1) (備考) 三角形の成立条件　ａ＞0・・・(1) 　ｂ＞0・・・(2) 　ｃ＞0・・・(3) 　ａ＋ｂ＞ｃ・・・(4) 　ｂ＋ｃ＞ａ・・・(5) 　ｃ＋ａ＞ｂ・・・(6) のうち，(4)(5)(6)から(1)(2)(3)が導かれるので，（例えば(4)(5)の辺々を加えるとｃ＞0となり(3)を得るなど）三角形の成立条件としては(4)(5)(6)で必要十分です. 　三角形の成立条件より（ｘ²-ｘ+1）＋（x²-2x）＞（2ｘ-1）・・<1> （x²-2x）＋（2ｘ-1）＞（ｘ²-ｘ+1）・・<2> （2ｘ-1）＋（ｘ²-ｘ+1）＞（x²-2x）・・<3> <1><2><3>よりｘ＞2 このとき， (ｘ²-ｘ+1)-(x²-2x)＝ｘ＋1＞0 （x²-2x）-（2ｘ-1）＝x²-4x+1の符号から　２＜ｘ＜２＋√3のとき（x²-2x）＜（2ｘ-1）　２＋√3＜ｘのとき（2ｘ-1）＜（x²-2x）（ｘ²-ｘ+1）-（2ｘ-1）＝ｘ2-3ｘ+2＝(ｘ-1)(ｘ-2)＞0 以上より 2＜ｘ＜2+√3のとき（x²-2x）＜（2ｘ-1）＜（ｘ²-ｘ+1）ｘ＝2+√3のとき（x²-2x）＜（2ｘ-1）＝（ｘ²-ｘ+1） 2＋√3＜ｘのとき（2ｘ-1）＜（x²-2x）＜（ｘ²-ｘ+1） (2)　△ＡＢＣの最大の内角はいくらか. （静岡大入試問題からの一部引用） 30° 45° 60° 90° 120° 135° 150°

4 　３辺の長さがx²+2x+4，x²-4，4x+4である三角形の最大角を求めよ. （桃山学院大学入試問題からの引用）	30° 45° 60° 90° 120° 135° 150°

(携帯版)...メニューに戻る

...（PC版）メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります