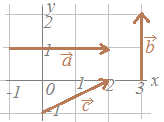|
○小中学校以来学んできたものの量は,単位が決まっていれば,大きさを表す数字を1つで表すことができました.
【例1】 身長 172.5(cm)
【例2】 体重 61.3(kg) 【例3】 面積 80(m2) ○これに対して,「力」「移動」「速度」のような量は,「大きさ」だけでなく「向き」も持った量で表されます.このように「大きさ」と「向き」を持つ量はベクトルと呼ばれ,1つの数字だけでは表せないので矢印を使って表されます. 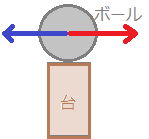 【例1】 力はベクトルで表されます
【例1】 力はベクトルで表されます
台の上のボールがどちらに落ちるかは,力の「大きさ」だけでなく,力の「向き」によって変わる.
 【例2】 移動はベクトルで表されます
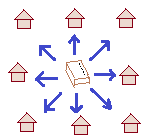
【例2】 移動はベクトルで表されます
荷物が届けられる家は,移動の「大きさ」(=距離)だけでなく,移動の「向き」によって変わる.
【例3】 速度はベクトルで表されます 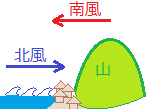
日本海沿岸では,風の速度の「大きさ」(=速さ)だけでなく,風の「向き」によって海の状態が変わる.
南風なら海は静かだが,北風なら海が荒れる. 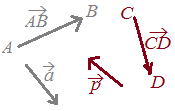 ベクトルの名前の付け方として,始点Aから終点Bに向かうベクトルは,
ベクトルの名前の付け方として,始点Aから終点Bに向かうベクトルは,で表します.
Bが左にあっても,
ベクトルを1つの名前で表すときは,などで表します. 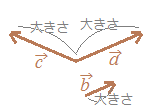 ○「矢印の向き」がベクトルの向きを表しており,「矢印の長さ」がベクトルの大きさを表しています.
○「矢印の向き」がベクトルの向きを表しており,「矢印の長さ」がベクトルの大きさを表しています.右図のベクトルについては, →右上に続く
|
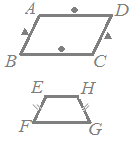
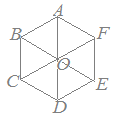
(1) 右図の平行四辺形ABCDにおいて,AD=BCかつAD//BC です.すなわち,ADとBCは同じ「向き」で「長さ」が同じです.したがって が成り立ちます. 同様にして も成り立ちます. しかし,ADとCBは「長さ」が同じですが「向きが逆」なので (2) 右図の等脚台形EFGHにおいて, 2.1) EHとFGは,「向き」が同じですが「長さが違う」ので 2.2) EFとHGは,「長さ」が同じですが「向きが違う」ので
【要点】
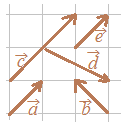
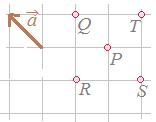
※(本気の雑談)○2つのベクトル と書く. ○2つのベクトルは,「大きさ」と「向き」さえ等しければ「等しい」といい,”どこに描いてあるか”は問題にしない. 例えば,上の図において 「向き」とよく似た用語に「方向」という用語があります.これらの用語の日常用語としての類似点・相違点については,ここでは述べませんが,高校数学で普通に使われる用語としての「向き」と「方向」の違いについて
ほぼ,次のように使い分けます.
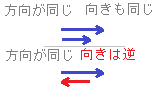 平行だったら「同じ方向」という. さらに,「あっち向き」「こっち向き」まで一致しているとき「同じ向き」という. したがって,「同じ向き」なら「同じ方向」になるが,「同じ方向」でも「同じ向き」と「逆向き」の区別がある. |
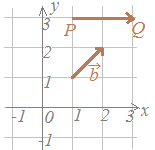 【例】
【例】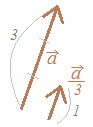 ※ベクトルの「向き」表す記号はないのか?
※ベクトルの「向き」表す記号はないのか?