<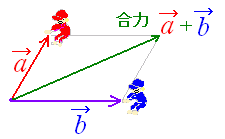 ■ 2つのベクトルの和を作図するには, (1) 上の例のように平行四辺形の対角線を作図する方法 の2つの方法があります.結果は同じですが,3個以上のベクトルの和を作図するなど,問題が複雑になると(2)の三角形の方が作図しやすいので,以下は三角形の方法で解説します. ■ 2つのベクトル , の和 + は、次の図のように、 の終点に の始点を重ねたときの の始点から の終点を結ぶベクトルで定義します。
|
< ■ 2つのベクトルの和を作図するには, (1) 上の例のように平行四辺形の対角線を作図する方法 の2つの方法があります.結果は同じですが,3個以上のベクトルの和を作図するなど,問題が複雑になると(2)の三角形の方が作図しやすいので,以下は三角形の方法で解説します. ■ 2つのベクトル , の和 + は、次の図のように、 の終点に の始点を重ねたときの の始点から の終点を結ぶベクトルで定義します。
|
|
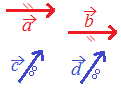
■問題 次の2つのベクトルの和に等しいものを右図から選びなさい. |
|
■[個別の頁からの質問に対する回答][ ベクトルの和について/18.7.24]
a→+b→=z→とした場合、|z→|= |a→|+|b→|なのですか?例えば、a→=2→、b→=3→の場合、2→+3→=5→なのですか?一般的にいうと|z→|つまり|a→+b→|=|a→|+|b→|は成り立ちますか?
■[個別の頁からの質問に対する回答][ベクトルの和について/18.1.16]
=>[作者]:連絡ありがとう.教材の内容と質問の内容が食い違っています.このページの危険な落とし穴というところを読んでください. 結論から言えば,全然違います.また質問にも使ってはいけない記号を使っていますので要注意です. a→+b→=z→とした場合、|z→|= |a→|+|b→|なのですか?は ベクトルの定数倍のところの図の→a+→bが始点+始点になっているので間違えいるとおもいます
■[個別の頁からの質問に対する回答][ベクトルの和について/17.5.25]
=>[作者]:連絡ありがとう.そのページはベクトルの和を扱っています.ベクトルの定数倍の質問ならベクトルの定数倍のページで質問すべきですが,どうやら質問者の書いている「定数倍」という言葉は,意味がないようです. おそらく,その前のベクトルの定義のページを十分読んでおられないと考えられます.すなわち「2つのベクトルは,「大きさ」と「向き」さえ等しければ「等しい」といい,”どこに描いてあるか”は問題にしない.」  そこで,「ベクトルの和を考えときは,終点に始点を接ぎ木して和を作ります」が,問題の図で終点に始点が接ぎ木してあるとは限らず,自分で移動させて作るのです.
そこで,「ベクトルの和を考えときは,終点に始点を接ぎ木して和を作ります」が,問題の図で終点に始点が接ぎ木してあるとは限らず,自分で移動させて作るのです.問題が図1のように書いてある場合に,それは問題が間違っているのではなく,問題を解く人が図2のように書き換えて答えを出すのです. 「ベクトルは,どこに描いてあっても構わないから移動させてよい」ということを理解するには,それなりに知的能力を必要としますが,これがクリアできなければ,ベクトルの和差などは理解できません. 第3問の問題ですが答えは、横軸X,縦軸Yとするならば座標(X,Y)にとして
始点座標(0,2)終点座標(2,2)ではないのでしょうか?
始点座標(2,0)終点座標(4,0)の回答絵を押すと正解のようですが、もしそうだとするなら どのように理解すればよいのか教えてください。
■[個別の頁からの質問に対する回答][ ベクトルの和について/17.2.9]
 =>[作者]:連絡ありがとう.ベクトルは「大きさ」と「向き」をもつ量として定義され,「大きさ」と「向き」さえ等しければベクトルとして等しいといいます.
=>[作者]:連絡ありがとう.ベクトルは「大きさ」と「向き」をもつ量として定義され,「大きさ」と「向き」さえ等しければベクトルとして等しいといいます.このことから注意すべきこととして,ベクトルにとっては「どこに書いてあるか」「始点がどこにあるか」はどうでもよいということになります. ご質問の(1) 始点座標(0,2)終点座標(2,2)というベクトルは「x軸の正の向き」に「大きさ2」です. ご質問の(2) 始点座標(2,0)終点座標(4,0)というベクトルは「x軸の正の向き」に「大きさ2」です. これら2つのベクトルは「大きさ」と「向き」が等しいので全く同じベクトルです.左の図において ※問題の趣旨としては,回答者がまず(1)の形でベクトルを作図するはずなので,それと「大きさ」と「向き」が等しいもの(2)が見つけられるか?という設定になっています. ※ベクトルに関する一連の教材の中で,ベクトルは「大きさ」と「向き」をもつ量として定義される,すなわち「どこに書いてあるか」「始点がどこにあるか」はどうでもよいという辺りの練習問題が足りませんでしたので,そのうち追加します. (追加しました) 還暦を過ぎ、学び直しています。
とても良く理解でき、解った自分に感激しています。
■[個別の頁からの質問に対する回答][ベクトルの和について/16.12.14]
=>[作者]:連絡ありがとう. 全く理解できませんでした()
=>[作者]:連絡ありがとう.それ以上やさしい教材は準備していません. |