=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック
◎内側の色を変えるには，次の色をクリック
◎標準文字色を変えるには，次の色をクリック

鼠

銀

黒

青

紺

茶

緑

桃

【2013年度センター試験.数学Ⅱ･B】第1問（必答問題）
〔1〕 Oを原点とする座標平面上に2点A(6, 0), B(3, 3)をとり，線分ABを2：1に内分する点をP，1：2に外分する点をQとする。3点O, P, Qを通る円をCとする。
(1)　Pの座標は( ア，イ )であり，Qの座標は
( ウ，エオ )である。

(1)
点Pの座標は
$({\displaystyle \frac{1\times 6+2\times 3}{2+1}},{\displaystyle \frac{1\times 0+2\times 3}{2+1}})$
$=({\displaystyle \frac{12}{3}},{\displaystyle \frac{6}{3}})=(4,2)$→ア,イ
点Qの座標は
$({\displaystyle \frac{-2\times 6+1\times 3}{1-2}},{\displaystyle \frac{-2\times 0+1\times 3}{1-2}})$
$=({\displaystyle \frac{-9}{-1}},{\displaystyle \frac{3}{-1}})=(9,-3)$→ウ,エオ
→解説を隠す←

(2)　円Cの方程式を次のように定めよう。線分OPの中点を通り，OPに垂直な直線の方程式は
y=カキx+ク
であり，線分PQの中点を通り，PQに垂直な直線の方程式は
y=x−ケ
である。
　これらの2直線の交点が円Cの中心であることから，円Cの方程式は
(x−コ)2+(y+サ)2=シス
であることがわかる。
(3)　円Cとx軸の二つの交点のうち，点Oと異なる交点をRとすると，Rは線分OAをサ：1に外分する。

(2)
O(0, 0), P(4, 2)の中点の座標は
$({\displaystyle \frac{0+4}{2}},{\displaystyle \frac{0+2}{2}})=(2,1)$
直線OPの傾きは
${\displaystyle \frac{2-0}{4-0}}={\displaystyle \frac{1}{2}}$
したがって，直線OPに垂直な直線の傾きは
−2
線分OPの中点を通り，OPに垂直な直線の方程式は
y−1=−2(x−2)
y=−2x+5→カキ,ク
P(4, 2),Q(9, −3)の中点の座標は
$({\displaystyle \frac{4+9}{2}},{\displaystyle \frac{2+(-3)}{2}})=({\displaystyle \frac{13}{2}},-{\displaystyle \frac{1}{2}})$
直線PQの傾きは
${\displaystyle \frac{-3-2}{9-4}}=-1$
したがって，直線PQに垂直な直線の傾きは
1
線分PQの中点を通り，PQに垂直な直線の方程式は
$y+{\displaystyle \frac{1}{2}}=x-{\displaystyle \frac{13}{2}}$
y=x−7→ケ
次の連立方程式を解く
y=−2x+5
y=x−7
解はx=4, y=3で円Cの中心(4, 3)と原点Oの距離は$\sqrt{4^2+3^2}=5$だから，円Cの方程式は
(x−4)2+(y−3)2=25
(x−4)2+(y−3)2=25にy=0を代入して得られる2つの解はx=0, 8
したがって，R(8, 0)
このとき，OR:RA=8:2=4:1 →解説を隠す←

【2014年度センター試験.数学Ⅱ･B】第1問（必答問題）
〔1〕 Oを原点とする座標平面において，点P(p, q)を中心とする円Cが，方程式$y={\displaystyle \frac{4}{3}}x$で表される直線ℓに接しているとする。 (1)　円Cの半径rを求めよう。
　点Pを通り直線ℓに垂直な直線の方程式は

y=−

ア

イ

(x−p)+q

なので，Pからℓに引いた垂線とℓの交点Qの座標は
$({\displaystyle \frac{3}{25}}($ウp+エq$),{\displaystyle \frac{4}{25}}($ウp+エq$))$
となる。
　求めるCの半径rは，Pとℓの距離PQに等しいので
$r={\displaystyle \frac{1}{5}}|$オp−カq$|$　･･･①
である。

(1)
　直線ℓの傾きは，$m={\displaystyle \frac{4}{3}}$だから，これに垂直な直線の傾きは，$m^{\prime }=-{\displaystyle \frac{3}{4}}$
　したがって，点Pを通り直線ℓに垂直な直線の方程式は
$y=-{\displaystyle \frac{3}{4}}(x-p)+q$→ア,イ
　次の連立方程式を解く
$y={\displaystyle \frac{4}{3}}x$･･･(#1)
$y=-{\displaystyle \frac{3}{4}}(x-p)+q$･･･(#2)
(#1)(#2)からyを消去すると
${\displaystyle \frac{4}{3}}x=-{\displaystyle \frac{3}{4}}(x-p)+q$
$16x=-9(x-p)+12q$
$25x=9p+12q$
$x={\displaystyle \frac{9}{25}}p+{\displaystyle \frac{12}{25}}q$
$={\displaystyle \frac{3}{25}}(3p+4q)$→ウ,エ
$y={\displaystyle \frac{4}{3}}\times {\displaystyle \frac{3}{25}}(3p+4q)$
$={\displaystyle \frac{4}{25}}(3p+4q)$
点P(p, q)から直線4x−3y=0に降ろした垂線の長さrは
$r={\displaystyle \frac{|4p-3q|}{\sqrt{4^2+(-3{)}^2}}}={\displaystyle \frac{|4p-3q|}{5}}$→オ,カ
→解説を隠す←

(2)　円Cが，x軸に接し，点R(2, 2)を通る場合を考える。このとき，p>0, q>0である。Cの方程式を求めよう。
　Cはx軸に接するので，Cの半径rはqに等しい。したがって，①により，p=キqである。
　Cは点Rを通るので，求めるCの方程式は
(x−ク)2+(y−ケ)2=コ　･･･②
または
(x−サ)2+(y−シ)2=ス　･･･③
であることがわかる。ただし，コ<スとする。
(3)　方程式②の表す円の中心をS，方程式③の表す円の中心をTとおくと，直線STは原点Oを通り，点Oは線分STをセする。セに当てはまるものを，次の⓪～⑤のうちから一つ選べ。

4p−3q=±5q（ただし，p, q>0）より
ア） 4p−3q=5qのとき
4p=8q
p=2q→キ
イ） 4p−3q=−5qのとき
4p=−2q
2p=−q→（p,q>0だから不適当）
ア）から円(x−2q)2+(y−q)2=q2は点R(2, 2)を通るから
(2−2q)2+(2−q)2=q2
4q2−12q+8=0
q2−3q+2=0
(q−1)(q−2)=0
q=1, 2
(p, q)=(2, 1), (4, 2)
したがって，求めるCの方程式は
(x−2)2+(y−1)2=1→ク,ケ,コ
または
(x−4)2+(y−2)2=4→サ,シ,ス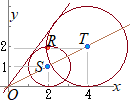
O(0, 0), S(2, 1), T(4, 2)について，点Oは線分STを1：2に外分する→④セ
→解説を隠す←