|
== 定積分で定まる定数 == Ⅰ 有理関数
(1.1)
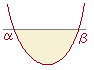
この定積分は,右図のように2次関数とx軸が2交点で交わるときに,2次関数とx軸とで囲まれる図形の面積(符号は負になっている)を表している.
高校数学Ⅱで発展学習として習うことがある.(教科書や授業では触れない場合もある) と書ける |
(証明) |
|
== 定積分で定まる定数 == Ⅰ 有理関数
(1.1)

この定積分は,右図のように2次関数とx軸が2交点で交わるときに,2次関数とx軸とで囲まれる図形の面積(符号は負になっている)を表している.
高校数学Ⅱで発展学習として習うことがある.(教科書や授業では触れない場合もある) と書ける |
(証明) |
|
(1.2)
前述(1.1)はこの公式において,m=1, n=1の場合になっている
(証明)次のように部分積分を行う. とおくと |
この漸化式を順次適用する ここで だから |
|
Ⅱ 無理関数
(2.1)
(2.2) 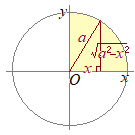 これらは高校数学Ⅲの置換積分で習う基本的な公式です.
これらは高校数学Ⅲの置換積分で習う基本的な公式です.(証明) (2.1)は右図の4分円の面積が円の面積
次のように置換積分を行います.
|
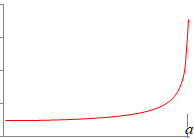 (2.2)
(2.2)のとき,この被積分関数は の極限値を求めます.
次のように置換積分を行います.
|
|
(2.3)
(2.4) 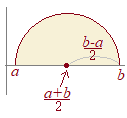 (証明)
(証明)(2.3) 2次関数に根号を付けたもので |
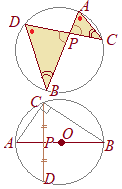 (参考) 方べきの定理
(参考) 方べきの定理右図上のように,弦ABとCDが点Pで交わるとき,△APCと△DPBが相似になることから,AP・BP=DP・CPが成り立つ. 右図下のように,CP=DPのときは,AP・BP=CP2となるから になる. CPは円周のy座標だから,その積分は半円の面積になる. (2.4) (2.3)と同様にして |
|
(2.5)
(2.6) 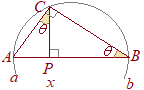 (証明)
(証明)(2.5) 右図のようにABを直径とする円において,∠CBP=θとおくと の辺々を掛けると 同様にして の辺々を掛けると (2)÷(1)により |
※区間の上端において広義積分になっているが,極限値を考えます. (2.6) 前問と同様にして |
| ■このサイト内のGoogle検索■ |