|
複素数平面上の線積分
※この分量の教材で,複素関数を初めから解説することは無理なので,そこまでは戻らない.一応,複素数や複素関数の初歩は分かるものとして進める.
あまり厳密な証明はせずに,簡単な例を見ながら,無理なく「真似できるようになる」ことを目指す. 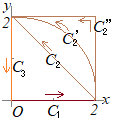 【例1】
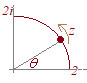
【例1】右図の複素数平面上の各点で関数が
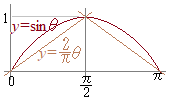
これは高校で習う実軸上の積分なので,問題なくできる
(3) 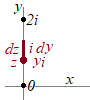
複素数
(重要)この問題のように,関数 
途中経路をCで表すと,この計算は
となることから分かるように「原始関数に対する始点と終点の値だけで決まり」「途中経路に依らない」 |
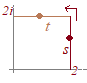
(2)
経路上の複素数
※1 前項の(重要)で書いたことは,ここでも言える.すなわち,このような複雑な変数変換によって実数の積分に直さなくても,複素関数としての不定積分が計算できるときは,その差で直接計算すればよい.(そこが複素関数の良い所!)※2 ここまでに求めた値を使えば,次項で述べるコーシーの定理(正則な領域における周回積分は0になること)を直接確かめることができる. 以上のことを,周回積分の記号を使って表すと となるが,このことは周回上の適当な点 (例えば原点)を始点かつ終点として積分を行えば となることからも分かる. |

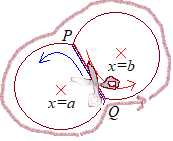 ※右図のように,閉曲線の中に2つの極があるとき,両方の曲を含む1つの閉曲線で周回積分を求めた場合
※右図のように,閉曲線の中に2つの極があるとき,両方の曲を含む1つの閉曲線で周回積分を求めた場合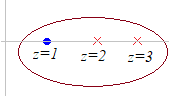
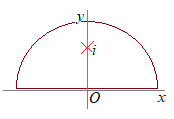
 (1) 例えば
(1) 例えば (2) また,例えば z=0に極(特異点)がある場合
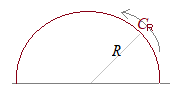
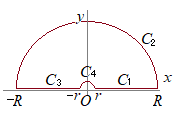
(2) また,例えば z=0に極(特異点)がある場合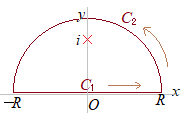 この積分を複素数平面上で留数定理を使って求めるには,右図のような周回積分を考えるとよい.
この積分を複素数平面上で留数定理を使って求めるには,右図のような周回積分を考えるとよい.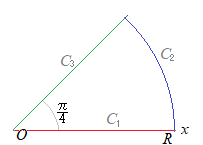 (証明)
(証明)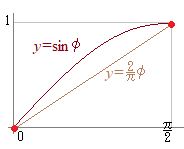
 (証明)
(証明)