Rの関数--入門レベル

hist(x, 		←数値から成るベクトル
	breaks= , 	←階級分けの境界となる数値
	right= ,  	←a<x≦b型 か a≦x<b型か
	xlim=c(始点, 終点), ←X軸の目盛りの範囲
	ylim=c(始点, 終点),←Y軸の目盛りの範囲
	main="",	←タイトル文字列
	xlab= "",	←X軸ラベル
	ylab= "")	←Y軸ラベル

主な引数
(1)第1引数には，ヒストグラムによって階級分けしてほしい数値のセットをベクトルで書く．

【例1】
x<-c(0.5, 1.2, 1.3, 2.4, 3.1, 3.2) #←6個の小数
hist(x)

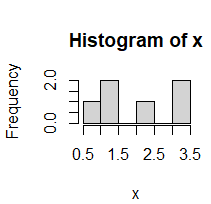　一般に，データの個数をNとするとき，分布の傾向を見やすくするための階級数kは，「スタージェスの公式」が目安とされている．

$k$ ≒ $\log_2N+ 1$

　幾つか具体例を挙げると，次の表のようになる．

N	1	2	4	8	16	32	64	128
k	1	2	3	4	5	6	7	8

　Rの関数hist()によって表示されるヒストグラムの階級数は，名前タグbreaks=によって指定され，デフォルト（省略された場合）では，breaks="Sturges"･･･すなわち，スタージェスの公式が適用される．ただし，上記の公式が機械的に適用されるのではなく，特に指定がなければ，10,20,50,100,200,500,...分割などになる．
　この例では，階級幅は0.5になっている．
(2)第2引数もしくは名前付き引数breaks=として，階級分けの境界となる数値（下端，上端も）をベクトルで書く．

【例2】
x<-c(0.5, 1.2, 1.3, 2.4, 3.1, 3.2)
hist(x, breaks=c(0, 1, 2, 3, 4))

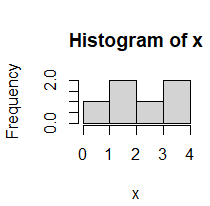　例2のようにbreaksを指定すると，右図のように整数で区切られた階級で表示される．
　なお，1,3,5, ..., 9のように初項1, 末項9, 公差2の等差数列を階級の境界線とするには
breaks=seq(1, 9, by=2)
　初項0, 末項4, 項数5の等差数列を階級の境界線とするには
breaks=seq(1, 9, length=5)

(3)　［危険な落とし穴あり！］　

ア）区間をa<x≦b型にとる場合は，right=TRUEもしくは right=Tもしくは省略
イ） a≦x<b型にとる場合はright=FALSEもしくはright=Fに指定する．

※以上のように，right=の指定を行わない場合（デフォルト，初期設定で，省略した場合） a<x≦b型の区間になる．これにより，整数値が境界線上にあるときに，日本の常識から見れば違和感のある分類になる．
　a<x≦b型で区間を設定するのは，ExcelのFrequency関数やピボットテーブルからのグループ分けにも登場する．アンダー18（18歳以下）で１つの階級を作るような分け方が西洋的かもしれないが，日本では20歳以上というように以上未満型（a≦x<b）の方をよく使う．
　だから，なるべくright=FALSEと指定する方がよいでしょう．このことは，次の例のように整数値のデータが登場する場合に，違和感を持たないために重要

【例3】
x<-c(1,2,2,2,3)
hist(x, breaks=c(0,1,2,3,4))

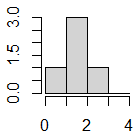　データでは2が3個あるはずであるが，ヒストグラムでは1が3個あるように見える．これは，right=の引数を省略した場合
0<x≦1, 1<x≦2, 2<x≦3, 3<x≦4の区間に各1,3,1,0個あるというグラフになっているから

【例4】
x<-c(1,2,2,2,3)
hist(x, breaks=c(0,1,2,3,4),right=F)

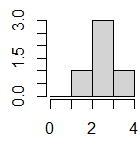　right=Fを指定すると，
0≦x<1, 1≦x<2, 2≦x<3, 3≦x<4の区間に各0,1,3,1個あるというグラフになる．日本では，この分け方が普通だから，right=Fと決める方がよい．

...（PC版）メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります