→ スマホ用は別頁
|
=== 読者が配色を変更したい場合 ===
《Rの関数の♪〜軽い解説》◎外側の色を変えるには,次の色をクリック
== 具体例で,とにかく動くもの == R version 4.0.3, 4.0.4Patched ----- この教材の最終更新年月日:2021.5.08
• この教材では,体験・入門のレベルで,「30分から1時間ほどでそこそこ分かるもの」「具体例による解説」を目指す.
• 本来,Rのコンソールから,help(キーワード)rとすうと,英文の解説が表示されるが,筆者にはやや苦痛を伴う. さらに,その英文の解説でGoogle翻訳を選ぶと,日本語で表示される[B]が,読みづらい.その表示される英文[A]をコピーして,Web上のGoogle翻訳に貼り付けると,[B]よりは読みやすい日本語になる[C]. • 論理的で正確なレファレンスが必要な人は,[A][B][C]などを読んでください. 関数 runif( )
一様分布(The Uniform Distribution)の疑似乱数を作る.
※正確には「疑似乱数」と言うべきであるが,疑似であることは了解されているものとして,以下においては単に「乱数」と書く.Rでは,一般に分布名をxxxとするとき,pxxx, dxxx, qxxx, rxxxにより各々密度関数,累積分布関数,クォンタイル関数,乱数関数という形で統一的に関数名が付けられる. 書き方 runif(n, min = 0, max = 1) |
主な引数 (1)第1引数には,発生させたい乱数の個数を書く. 第1引数だけを指定し,第2引数以下を省略した場合,min=0, max=1として,0以上1以下の小数の乱数が返される.
【例1】
(2)第2引数には発生させたい乱数の下限を,第3引数には上限を書く.runif(1) ⇒ 0.1847987など(結果は毎回変わる) runif(3) ⇒ 0.7224764 0.8229446 0.2895083など3個の乱数が返される
【例2】
※例2の結果は,runif(2, 2, 3)*10と同じになる.runif(2, 20, 30) ⇒ 22.47484 28.57085 (20以上30以下の小数の乱数が2個返される) (ベクトルの定数倍は,各成分を定数倍したベクトルになる:c(x1, x2,・・・, xn)*k → c(kx1, kx2,・・・, kxn) )
|
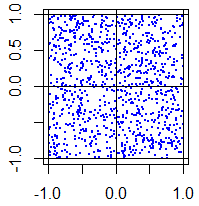 (結果)
(結果)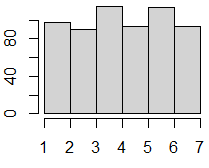 (結果)
(結果)