|
【内分点】
(解説)m, nを正の数とするとき,異なる2点z1 , z2をm:nに<内分する点を表す複素数は 特に,1:1に内分する点(中点)を表す複素数は
図1
原点からz1 , z2をm:nに<内分する点まで進むには,図1のように,まずz1まで進み,次に内分点まで進めばいよい.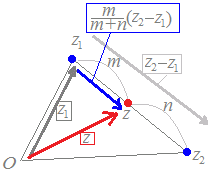 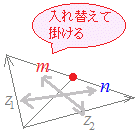 (初歩的な注意1)
(初歩的な注意1)z1からの比率がmで,z2からの比率がnのときに,この公式の分子は nz1+mz2 という形で,「遠い方の比率と掛ける」ようになっていることに注意 (初歩的な注意2) この内分点の公式の公式で与えられる複素数は,上の図1において青の矢印で示したようなものを表しているのではなく,赤の矢印で示したように原点からその内分点に向けられたものを表していることに注意 ここで,z1からz2に向かう移動は(終点)-(始点)により z2−z1 だから,z1から内分点に向かう移動は,それを 倍にしたもの. したがって, (z2−z1 )倍 結局 z=z1+(z2−z1 ) = =
【例1】
2点z1=1+2i,z2=4−iを1:2に内分する点を表す複素数は z===2+i 図は次の通り 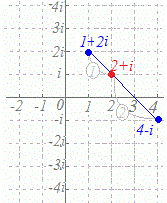 |
|
【例2】
2点z1=−1−3i,z2=3+iの中点を表す複素数は z===1−i 図は次の通り 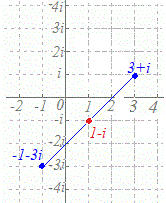 |
|
問題1次の各点を表す複素数として,正しいものを選んでください. |
|
内分公式に代入すると
==1+3i |
|
内分公式に代入すると
==1+i |
|
==−1+2i |
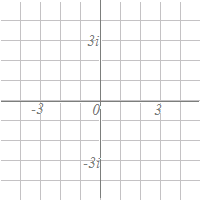
問題2次の図において青で示した点 はz1を,赤で示した点 はz1を,赤で示した点 はz2を表しています.このとき,各々指定された点をポイントしてください. はz2を表しています.このとき,各々指定された点をポイントしてください.全部で5題あります→ [第1問 / 全5問] 解説 NEXT 
|
問題3次の図において青で示した点 はz1を,赤で示した点 はz1を,赤で示した点 はz2を表しています.このとき,各々指定された点を『目分量で』ポイントしてください. はz2を表しています.このとき,各々指定された点を『目分量で』ポイントしてください.全部で5題あります→ [第1問 / 全5問] 解説 NEXT 

|
|
【外分点】
(解説)m, nを正の数とするとき,異なる2点z1 , z2をm:nに外分する点を表す複素数は (ただし,外分については,1:1の外分は考えない.) 例えば,線分ABを2:1に外分する点Pとは,線分ABのBの延長上(外側)に点をとって,AP:BP=2:1となる点Pのことをいいます.
図2のような間違いがよく見られますので注意してください.「ABを2:1に外分する点P ⇒ AP:BP=2:1」というとき,片足は必ずPになっていなければなりません.
図2
一般に,線分ABをm:nに外分する点は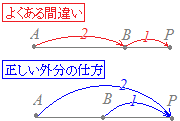 ア) m>n (ただし,m>0, n>0)のとき
図3のように,線分ABの延長上でAP>BPとなる点Pは,Bの外側にきます.
A(z1), B(z2), P(z)とおくと, z=z1+(z2−z1 )= =
図3
イ) m<n (ただし,m>0, n>0)のとき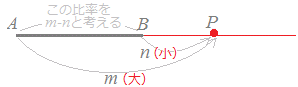
図4のように,線分ABの延長上でAP<BPとなる点Pは,Aの外側にきます.
A(z1), B(z2), P(z)とおくと, z=z1+(z1−z2 )= ==
図4
※外分比が等しいとき(すなわちm=nのとき ⇒ 1:1, 2:2など)は,分母が0となって,「おかしい」ことがわかる.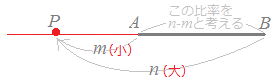 図3の場合はmの方が大きくなり,図4の場合はnの方が大きくなり,どちらの場合でもmとnが等しくなることはない. このように,1:1の外分だけはない. |
|
【分点の公式のまとめ】
※(覚え方)
m, nを実数とするとき,異なる2点z1 , z2をm:nに分ける点を表す複素数は m,nが同符号の場合は内分点を表し,異符号の場合は外分点を表す. (ただし,m=−nの場合は考えない.) 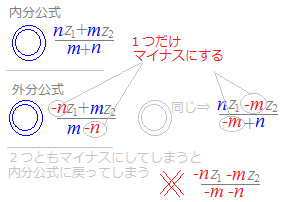 |
|
(参考) m:nをk:1で表したときのkの値と分点の場所 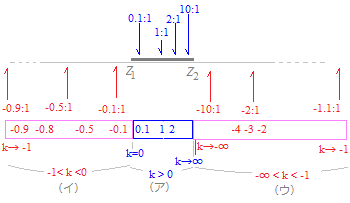 (イ) −1<k<0のときはz1の外側の外分点になる. (イ) −∞<k<−1のときはz2の外側の外分点になる. |
|
問題4次の各点を表す複素数として,正しいものを選んでください. |
|
外分公式に代入すると
=−1−i−4+6i=−5+5i |
|
外分公式に代入すると
==−2+3i |
問題5次の図において青で示した点 はz1を,赤で示した点 はz1を,赤で示した点 はz2を表しています.このとき,各々指定された点を『目分量で』ポイントしてください. はz2を表しています.このとき,各々指定された点を『目分量で』ポイントしてください.全部で5題あります→ [第1問 / 全5問] 解説 NEXT 

|