← PC用は別頁
|
関数f(x)の不定積分の1つ(1つの原始関数)をF(x)とするとき、すなわち次の関係を満たすとき
F(x)=f(x) ⇔ f(x) dx=F(x)+C
定積分は不定積分の値の差で定義される
f(x) dx=F(b)−F(a) ※初めて習うときに、引き算の仕方を間違う人が時々いるので注意。F(a)−F(b)ではない。
[解説]f(x) dxの形の式を定積分という。 ここで、aを定積分の下端、bを定積分の上端という。 数学II で習ったように、f(x)≧0となる区間においては、定積分はその関数とx軸とで囲まれた図形の面積を表す。
図1
定積分では、この図形の面積を図2の2つの図形の面積の差として表していることになる。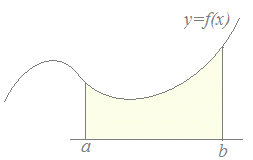
図2
ここで、不定積分F(x)+Cは図3のように区間の上端(右端)を変数xで表したときに、xよりも左にある図形の面積を表しており、bの左にある図形の面積からaの左にある図形の面積を取り除くとa, bの間にある図形の面積になるというのがこの定積分の図形的な意味になる。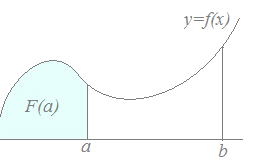 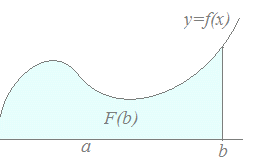
図3
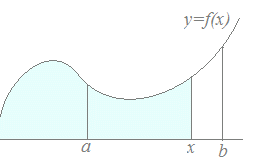
定積分の計算は、f(b)−f(a)のように関数f(x)に直接値を代入するのではなく、一旦不定積分F(x)を求めてからこれに代入することになるので、2段階の操作になる:F(b)−F(a)
結局、定積分は次の形で使われる。
そこで、この計算をスムーズに行えるように「まず不定積分F(x)を求めて」「次に、a, bを代入する」ということを表すために F(x) という記号を使う。
f(x) dx=F(x)=F(b)−F(a)
例図4において、関数y=x2とx軸、およびx=a, x=bで囲まれた図形の面積を求めるには、次のように計算する。 x2 dx= = − =
図4
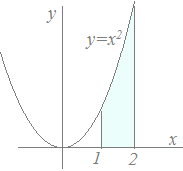 不定積分の積分定数Cは0とする[次の解説参照]。 |
|
※ 歴史的には、区分求積法(数列の和Σの極限)として定積分が先に登場した。
和ΣはSum→その極限を表すためにSを縦に伸ばしてという記号を使う。
数列の和から定積分を求めるには込み入った計算を要するが、微分の逆:不定積分を使うと簡単に求められることが分かった。現在の教育課程では、これらの結果を分かりやすく並べ替えて「不定積分を用いて定積分を定義する」ようになっている。※ ある区間で連続な関数については、定積分が定義できる…不連続関数の定積分は、取り扱いが難しくここでは扱わない。(高校ではほとんど登場しない) ※ 定積分の計算をするときに、不定積分で登場する積分定数Cは引き算のときに消えてしまう。 例えば、x2の1つの不定積分を+1とした場合、+2とした場合、一般に+Cとした場合、各々の計算は次のようになる。 x2 dx= +1 =( +1)−( +1)= x2 dx= +2 =( +2)−( +2)= x2 dx= +C =( +C)−( +C)= このように
定積分の計算においては、不定積分に登場する積分定数Cの値としてどの値を使っても同じになるので、計算が最も簡単になるようにC=0とするのが常識
|
|
○2 定積分の計算例 不定積分の関数形が分かれば、定積分は 代入して差を求めるだけで計算できる。
(1)
= log|x+1|=log6−log2=log3
(2)
dx= x = 9 − 4 = dx
(3)
e2xdx= = − = e2xdx |
|
(4)
logx dx= xlogx−x = (2log2−2)−(0−1)logx dx =2log2−1 logx dx=xlogx−x+Cの計算は普通は部分積分で求める。ただし、何度も使うと覚えてしまうことがある・・・覚えてしまっていたら使ってもよい。
(5)
cos 2x dx= = 0−0=0cos 2x dx |
|
○3 定積分の性質 定積の性質には「(I) 不定積分の性質をそのまま引きずっているもの」と「(II) 下端、上端に関するもので不定積分にはない性質」とがある。
(I)不定積分と同様の性質が成り立つもの
1. kf(x)dx=kf(x)dx …(kは定数) 2. {f(x)+g(x)}dx=f(x)dx+g(x)dx 3. {f(x)−g(x)}dx=f(x)dx−g(x)dx (II)下端、上端に関するもの(定積分だけの性質) 1. f(x)dx= −f(x)dx 2. f(x)dx=0 3. f(x)dx+f(x)dx=f(x)dx (I) 1. 2.3. ←番号をクリック (II) 1. 2. 3. ←番号をクリック |
|
■問題1 次の空欄に入るものを右の選択肢から選びなさい。 (はじめに左の空欄?を1つ選び、続いて右の選択肢を選びなさい。正しければ代入され、間違っていれば元に戻ります。)
(1)
(x+ )dx
= = ··· = +log2 (2) = ( − )dx = = ··· (3) dx = = ··· (4) = = ··· (5) dx = = ··· (6) |x|dx = = ··· (7) |x−1|dx = = ··· (8) |sin x|dx = = ··· |
|
■問題2 次の定積分の値を求めてください. ★無理関数
(1)
解答を見る
(2)
解答を見る |
|
★分数関数
(3)
解答を見る
(4)
解答を見る |
|
★三角関数
(5)
解答を見る
(6)
解答を見る |
|
★絶対値記号
(7)
解答を見る
被積分関数に絶対値記号が付いているときは,区間を分けて絶対値記号を外してから積分します
ア) イ) \(\displaystyle \int_0^{2\pi}\mid \sin x\mid dx\) \(\displaystyle =\int_0^{\textcolor{red}{\boxed{\pi}}}\mid \sin x\mid dx+ \int_{\textcolor{red}{\boxed{\pi}}}^{2\pi}\mid \sin x\mid dx\) (原式)
この問題の結果(*1)は,定積分の結果に絶対値記号が付いているもの(*2)とは全く別のものなので注意
(8)
解答を見る |
|
(9)
解答を見る |
|
|
|
■[個別の頁からの質問に対する回答][定積分の基本について/17.5.25]
図3の下の紫色の囲みの式について、
F(b-a) という風に代入すると楽になると学校で教わったのですが、そうするとF(b)-F(a) で計算するときと答えが合わなくなります。
F(b-a)は間違いですか?
■[個別の頁からの質問に対する回答][定積分について/17.2.22]
=>[作者]:連絡ありがとう.一般に「F(b-a) という風に代入すると楽になると学校で教わった」ことはないでしょう.ノートの写し間違いでしょう. そのようなことが言えるのはf(x)が定数になっているような特別な場合,すなわちf(x)=k → F(x)=kx → F(b)−F(a)=kb−ka=F(b−a)となるような場合だけです. めちゃくちゃありがたいです!
すごく助かってます!
■[個別の頁からの質問に対する回答][定積分について/17.2.10]
=>[作者]:連絡ありがとう. 問題があるのはとてもいいけど問題が変わるようにしてほしい!
=>[作者]:連絡ありがとう. |