|
�y�悭�g�������ꗗ�z
(1) �萔���̘a �@�@���� (2) �P�����̘a (3) �Q�����̘a (4) �R�����̘a |
|
�y�悭�g�������ꗗ�z
(1) �萔���̘a �@�@���� (2) �P�����̘a (3) �Q�����̘a (4) �R�����̘a |
|
�y����z (1)←
�i�Q�l�j
�Ȃ��C�ϕ��i�a�̋Ɍ��j�Ƃ̑Ή��ɂ��� �����藧���Ƃ́C�܂��������Ȃ��ł��傤�D �Ƃ��낪�C �����藧�ƁC���ȏ��ɖ����I�ɏ�����Ă���̂ɑ��āC���̋��ȏ��ł� �Ə�����Ă��܂��D ��v���
|
|
�y��1-1�z�@���̎����ȒP�ɂ��Ă��������D
�i�j
�y��1-2�z�@���̎����ȒP�ɂ��Ă��������D
�i�j
�y��1-3�z�@���̎����ȒP�ɂ��Ă��������D
�i�j |
|
�y���P�z�@���̘a�����߂Ă��������D�i�I�����̒����琳�������̂��P�N���b�N�j
(1)
|
|
(2)
|
�y����z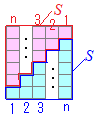 (2)←
(2)←�͏���1�C����1�C�������̓�������̘a������C�E�}�̂悤�ɗ������̂��̂Ƒg�ݍ��킹��ƁC�S�̘̂a�̂Q�{�̂��̂��C�cn+1�~��n��=n(n+1)�ɂȂ�D ����������
�y��2-1�z�@���̎����ȒP�ɂ��Ă��������D
�i�j�������̌`����������̘a�́C���̌������g���āu�W�J���āC���ɂ��������g�ݍ��킹�ċ��߂�v�̂���{�ł��D
�y�����z
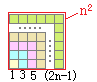
����O�I�Ɂu�K�i��̊��v�ɂȂ��Ă�����̂ȂǁC���܂�������������̂ɂ��Ă͌�ŏq�ׂ܂��D
�y��2-2�z�@���̎����ȒP�ɂ��Ă��������D
�i�j�������̌`����������̘a�́C���̌������g���āu�W�J���āC���ɂ��������g�ݍ��킹�ċ��߂�v�̂���{�ł��D
�y�����z
�������ŁC�u����Ȍ����͏K���Ă��Ȃ����v�ƌ������鐶�k�����āC���������Ƃ�����܂��D
�������Ȃ�C���̂悤�Ȃ��Ƃ́u�����I�Ɂv�����܂��D�i���R�ł��I�j ���������āC �i�����j |
|
�y���Q�z�@���̘a�����߂Ă��������D�i�I�����̒����琳�������̂��P�N���b�N�j �����Q�Ȍ�̖��͈ÎZ�ł͖����ł��D�v�Z�p���Ōv�Z���Ă��瓚���Ă��������D
(1)
|
|
(2)
|
|
�y����z (3)← �A�j ��ʂɁC���{�P�����ׂ̗荇���Q���̍����C�������ɂȂ邱�Ƃ𗘗p���āC�������̘a�����߂邱�Ƃ��ł��܂��D ������Ă݂�ƁD ……… ���Ȃ킿 ���� ���������� ���̎���ό`����� |
|
�y��3-1�z�@���̎����ȒP�ɂ��Ă��������D
�i�j�������̌`����������̘a�́C�u�W�J���āC���ɂ��������g�ݍ��킹�ċ��߂�v�̂���{�ł��D
�y��3-2�z�@���̎����ȒP�ɂ��Ă��������D
�i�j�������̌`����������̘a�́C�u�W�J���āC���ɂ��������g�ݍ��킹�ċ��߂�v�̂���{�ł��D k������ϐ��Ƃ��郰�L���̓����ł́C���͒P�Ȃ�萔�Ƃ��Ĉ����܂��D�i�O�ɏo�����ʂł͕ϐ��ł��j |
|
�y���R�z�@���̘a�����߂Ă��������D�i�I�����̒����琳�������̂��P�N���b�N�j
(1)
|
|
(2)
|
|
(3)
|
|
�y����z (4)← �A�j�@ �����������Ƃ���C �ł��D �C�j�@�a�����߂₷���K��^���𗘗p������@�́C���̃y�[�W�Ɏ����Ă��܂��D �E�j�@���w�I�A�[�@���g���C���̂悤�ɏؖ��ł��܂��D �i�T�jn=1�̂Ƃ� ������ �͐�������D �i�U�jn=m�im��1�ȏ�̐����j�̂Ƃ� ����������Ɖ��肷��ƁC ���ӂ� �i���Ӂj �i�E�Ӂj ����āCn=m+1�̂Ƃ�����������D �i�T�j�i�U�j���C���ׂĂ̎��R��n�ɂ��Đ�������D |
|
�y��4-1�z�@���̎����ȒP�ɂ��Ă��������D
�i�j�������̌`����������̘a�́C�u�W�J���āC���ɂ��������g�ݍ��킹�ċ��߂�v�̂���{�ł��D
�y��4-2�z�@���̎����ȒP�ɂ��Ă��������D
�i�j�������̌`����������̘a�́C�u�W�J���āC���ɂ��������g�ݍ��킹�ċ��߂�v�̂���{�ł��D k������ϐ��Ƃ��郰�L���̓����ł́C���͒P�Ȃ�萔�Ƃ��Ĉ����܂��D�i�O�ɏo�����ʂł͕ϐ��ł��j |
|
�y���S�z�@���̘a�����߂Ă��������D�i�I�����̒����琳�������̂��P�N���b�N�j
(1)
|
|
(2)
�W�J���Ă��ł��܂����C�K��^���ɂ��ẮC�P���������̍��ŕ\���ĊȒP�ɋ��߂���@������܂��D
������ k=1���� k=2���� ……… k=n���� �ӁX������� |
|
�y���ʂłȂ��������o���Ă��������悢���́z
(5)�@ ���䐔��̘a (6)�@ (����)�~(����)�`�̐���̘a (7)�@ f(n)−f(n−1)�`�̐���̘a�F�K��^�����܂� |
|
�y����z (5)← ���L�����瓙�䐔��̘a�����߂�ɂ́C
����a�C����r�C����n�̂R�v�f�ɕ����ēǂݎ��C�u���䐔��̘a�̌����v
�ɑ������悤�ɂ��܂�. …(*) …(*) |
|
�y��5-1�z�@���̎����ȒP�ɂ��Ă��������D
�i�j���������߂�ɂ́Ck=1�������܂��D ��������߂�ɂ́C ����C�����2�ł��邱�Ƃ�������܂��D ���������߂�ɂ́Ck=1����n−1�܂ʼn������邩���ׂ܂��D n−1 �ȏ�ɂ��C���߂铙�䐔��̘a��
�y��5-2�z�@���̎����ȒP�ɂ��Ă��������D
�i�j���������߂�ɂ́Ck=1�������܂��D ��������߂�ɂ́C ����C�����1/2�ł��邱�Ƃ�������܂��D ���������߂�ɂ́Ck=1����n�܂ʼn������邩���ׂ܂��D n �ȏ�ɂ��C���߂铙�䐔��̘a�� |
|
�y���T�z�@���̘a�����߂Ă��������D�i�I�����̒����琳�������̂��P�N���b�N�j
(1)
���������߂�ɂ́Ck=1�������܂��D
��������߂�ɂ́Ck=1, 2, 3, … �������āC���ꂼ�ꉽ�{�ɂȂ邩���ׂ܂��D ����C�����3�ł��邱�Ƃ�������܂��D ���������߂�ɂ́Ck=1����n�܂ʼn������邩���ׂ܂��D n �ȏ�ɂ��C���߂铙�䐔��̘a�� |
|
(2)
���������߂�ɂ́Ck=0�������܂��D
��������߂�ɂ́Ck=0, 1, 2, 3, ···�������āC���ꂼ�ꉽ�{�ɂȂ邩���ׂ܂��D ����C�����2�ł��邱�Ƃ�������܂��D ���������߂�ɂ́Ck=0����n−1�܂ʼn������邩���ׂ܂��D�i1����n−1��n−1������0����n−1��n�j n �ȏ�ɂ��C���߂铙�䐔��̘a�� |
|
�y����z (6)← ���̃y�[�W��ǂ�ł��������D (7)← ���̃y�[�W��ǂ�ł��������D |
|
�y��6-1�z�@x��1�̂Ƃ��C���̘a�����߂Ă��������D
�i�j�Ƃ����� ������ �����̏ؖ��́C����� �Ƃ��āC���ӂ�������Ă�������D
�y��6-2�z�@���̘a�����߂Ă��������D
�i�j�A�jx=1�̂Ƃ� �́C������1�C������2�C������n�̓�������̘a������ �C�jx��1�̂Ƃ� �̂Ƃ� ������ �����̏ؖ��́C�y��6-1�z�̌��ʂ��g���Ă��ł��܂��D ��ʕ�����ł��܂��D |
|
�y��7-1�z�@���̘a�����߂Ă��������D
�i�j������ �̂悤�ɒ��ԍ��������邩��
�����̖��́u�������������ɂ���@�v�̓���I�Ȃ��̂ł����C�P�Ɂu�������������v���Ȃ���،^�ɈËL���Ă���Ɨ��Ƃ���������܂��D
���m�ɂ́C���̕��� �̕��ꂪ���̂Q����������C���̕����͂��́|�Q�����D �����ŁC�ϕ��v�Z�̂Ƃ��ɁC���n���Ƃ��Ď������P���������������Ă���Ƃ����v�������ׂȂ���C�u���́|�Q�����v�̎������P�����������l����Ɓu���́|�P�����v�ƂȂ� ���̎��ŗׂ̍� �Ƃ̍��ŕ\���Ƃ������Ƃł��D ������ �Ƃ���ƁC��L�̂悤�����ԍ��������邩���C�ȒP�ɂȂ�̂ł��D �����̒��ӏ����́C���̂悤�ȕ��ꂪ�R���̐ςɂȂ��Ă���ꍇ��C�����ł͂Ȃ��������̐ςɂȂ��Ă���ꍇ�ɃY�o�����Ă͂܂�܂��D �Ƃ���̂ł͂Ȃ� �Ƃ���D �Ƃł���D�i��̉���Q�Ɓj
�y��7-2�z�@���̘a�����߂Ă��������D
�i�j
���ꂪ���̂Q�����C�����S�̂͂��́|�Q����������C���́|�P�����̍��ŕ\���D
�ƂȂ邩�� |
|
�y��7-3�z�@���̘a�����߂Ă��������D
�i�j
���ꂪ���̂R�����C�����S�̂͂��́|�R����������C���́|�Q�����̍��ŕ\���D
�K���Q�̕����̍��ɂ��邱�ƁD�R�̕����ɕ����Ă��܂�����C�v���X�R�c�ƃ}�C�i�X�R�c�̂ǂ��炩�������Ȃ邩��C���ԍ��������Ȃ����Ƃɒ��� �ƂȂ邩��
������Ȃ������́C��P�C��Q�̂悤�ɏc�����ɂ���ƁC���S�m���ɒ��ԍ��������邪�C�Q�l���Ȃǂł͎��̂悤�ɃX�}�[�g�Ɏd�グ�邱�Ƃ������D�������������v�Z���Ă���̂����������Ă�����C�^������̂��悢�D
�y��7-4�z�@���̘a�����߂Ă��������D
�i�j
�������������Ƃ�����،^�̈ËL�����ł́C���̖��̉���������L�Ɠ������Ƃ������ƂɋC�t���Ȃ����C���͓����D
���̂Q����������C���̂R�����̍��ŕ\���D ������ ��������ɂ����Ƃ��́C�Ă��˂��ɏc�����ɂ���ƁC������ׂ����ԍ��������܂��D ����ʂɊK��^���̘a�́C�P�������̍����K��^���ɂȂ�D |
|
�y��7-5�z�@���̘a�����߂Ă��������D
�i�j
���̂R����������C���̂S�����̍��ŕ\���D
�̂ݎ����F
�y��7-6�z�@���̘a�����߂Ă��������D
�i�j������ |