← PC�p�͕ʕ�
|
← PC�p�͕ʕ�
�y�t���̋��ߕ��z
�@�@�i�h)�@y= … �̌`�̎��� x= … �̌`�ɉ����D �@�@�i�U�j�@�Ɨ��ϐ��� x �ŕ\�킷�K���ɏ]���āC�ϐ� x , y ����ꊷ����D �y�t���̋L���C��`��E�l��z �@�@�i�P�j�@�� f(x) �̋t���� f −1(x) �ŕ\�킷�D �@�@�i�Q�j�@������Ƃ��̋t���Ƃł́C��`��ƒl�悪����ւ��D �y�t�������݂��邽�߂̏����z �@�@�@�� y=f(x) �̋t�������݂��邽�߂ɂ́C�� y=f(x) ���P�P�̊��łȂ���Ȃ�Ȃ��D �@�@�@���Z�ň������Ō����C�u�P���������v�܂��́u�P���������v������ɑΉ�����D �y�t���̐����z �@�@�@����� y=f(x) �̃O���t�Ƃ��̋t�� f −1(x) �Ƃ� y=x �̒����Ɋւ��đΏ̂ɂȂ�D �@�@�@����� y=f(x) �̂��̋t�� f −1(x) �Ƃ���������ƁC�P���� I(x)=x �ɂȂ�D |
| ���@�t���Ƃ� ���@�� y=2x+1 ���l���Ă݂�ƁCx �̒l�� y �̒l�͎��̕\�P�̂悤�ɑΉ����Ă���D
�@�\�P�Ƌt�̑Ή����l����ƁC�\�Q�̂悤�ɂȂ�D
�@�\�Q�̑Ή������ŏ����� y= �@���̂Ƃ��C�� y= ���C���̊� y=2x+1 ���t���Ƃ����D |
���@�t���̋��ߕ�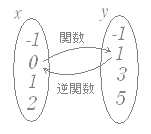 �@���}�P�̂悤�ȑΉ����l����ƁCy �̒l���� x �̒l�ւ̑Ή������߂�悢�̂�����C �i�h�j y=2x+1�@��ό`���ā@x= �ɂ���D�i�`�͂���ŋ��܂��Ă���j �i�U�j�@�ʏ�C�Ɨ��ϐ��� x �ŁC�]���ϐ��� y �ŕ\�킷�K���ɏ]���āC�ϐ� x , y ����ꊷ����ƁC y=�@�i�K���̖��j �@����āC�� y=2x+1 �̋t���� y=
�@�y�t���̋��ߕ��z
�i�h)�@y= … �̌`�̎��� x= … �̌`�ɉ����D �i�U�j�@�Ɨ��ϐ��� x �ŕ\�킷�K���ɏ]���āC�ϐ� x , y ����ꊷ����D �� �@y=−1 �̋t�������߂�ɂ� �i�h�j�@x �ɂ��ĉ����Ɓ@3y=x−3 �� x=3y+3 �i�U�j�@�ϐ� x , y �����ւ���� y=3x+3 …�i���j |
|
�i���䗠1�j �@y=2x+1 …(1) �� x= …(2) �Ƃ͓����W���ł���D �@����́C(2)�̗��ӂ�2�{����1�������(1)�ɖ߂邱�Ƃ����������D �@�ł́C���̊��Ƃ��̋t���̈Ⴂ���o�錮�͂ǂ����琶�����̂��ƍl����ƁC�i�U�j�̕ϐ��̓��ꊷ���������ɂȂ��Ă���D
y=2x+1 �����l�� x=
�t���@���� y= �@�������C�t���́u�`�v�́i�h�j�̒i�K�Ŋ��S�ɓ����Ă���D �i���䗠�Q�j �@��L�́i�h�j�i�U�j�̏������t�ɂ��Ă��悢�ƍl�����邪�C���ۂɍ��Z��������������ʂ��l���Ă݂�ƁC�i�h�j�i�U�j�̏��̕����ԈႢ�����Ȃ��D �@���Ȃ킿�C�Ō�� y= … �̌`�ɂ���Ƃ���C�r���̕ό`�����G�ɂȂ�ꍇ�ɔ������C�u���߂� �i�U�j x , y ����ꊷ���āC���Ɂi�h�j y �ɂ��ĉ����v�ƍl����C�������ƂɂȂ�͂������C���Z�������������Ƃ��̓X���[�Y�ɍs���Ȃ��悤�ł���D ��P y=2x+1 ���U�� x=2y+1 ���h�� y= �͂��܂��s���D ��Q y=(x−1)2+3�@�i x��1 �j�� x=(y−1)2+3�@�i y��1 �j����`��ł͂Ȃ�!! �����ō���!! |
| ���@�t����\�킷�L���C��`��ƒl�� �i�P�j�@�� f(x) �̋t���� f −1(x) �ŕ\�킷�D
�@�@�@���@f(x)=2x+1 �̂Ƃ��Cf −1(x)= �i�Q�j�@������Ƃ��̋t���Ƃł́C��`��ƒl�悪����ւ��D �@�@�@���@y=2x+1 �i 1��x��4 , 3��y��9 �j�̂Ƃ��C �@�@�@�@���̋t���� y= �i 3��x��9 , 1��y��4 �j ���@���̒�`�悪��������Ă��Ȃ��Ƃ��́C���̊�����`�ł���ł��L���͈͂��l���C�Ή�����l���l��Ƃ���D ���@f(x)=2x+1 �� x �͑S�����Cy �͑S���� ���@f(x)= �� x��2 , y��0 ���@f(x)= �� x��2 , y��0 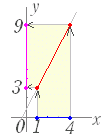 �i�Q�j�ɂ���
�i�Q�j�ɂ����@y=2x+1 �i 1��x��4 , 3��y��9 �j�̂Ƃ��C ����� �@�i�h�j x �ɂ��ĉ����Ă��C x , y �̊W���Ƃ��Ă͓������̂ŁC��`��C�l�悪����ւ�錴���͂����ɂ͂Ȃ��D
�@y−1=2x �i 1��x��4 , 3��y��9 �j
�@x= �i 1��x��4 , 3��y��9 �j �i�U�j�̑���ŕ��� x , y �����ւ��邩��C��`��ƒl�悪����ւ��D �@y= �i 1��y��4 , 3��x��9 �j �@��`����ɏ����� �@y= �i 3��x��9 �C1��y��4�j |
|
�i���䗠�R�j �i�P�j�ɂ��� �@ f −1(x) ���P�̋L���ł����āC ��\�킷��ł͂Ȃ��C f −2(x) �Ƃ����L�������Z�ł͎g��Ȃ��D �i f(x)=2x+1 �̂Ƃ��Cf −1(x)=���j �@�O�p�� y=sin x �̋t�� sin−1x ��s�� A �̋t�s�� A−1 �̋L��������Ɠ��l�D �i���䗠�S�j �i�Q�j�ɂ��� �@�i�U�j�̑���ŕ��������ւ���̂ŁC���̕����ɒ����Ă���͈́i��`��ƒl��j���ς�D |
|
���@�t�������݂��邽�߂̏��� �@�� y=f(x) �̋t�������݂��邽�߂ɂ́C�� y=f(x) ���P�P�̊��łȂ���Ȃ�Ȃ��D�i��萳�m�ɂ́C�u��ւ̂P�P�̊��v�j
�@���Z�ň������Ō����C�u�P�������v�܂��́u�P�������v�̋�Ԃ��`��Ƃ���t�������݂���D �@��������������`�ł��邽�߂ɂ́C�e�X�� x �̒l�ɑ��đΉ����� y �̒l���������܂�Ȃ���Ȃ�Ȃ��D
�i x �� y ���C�ʏ�̈Ӗ��ł̊��łȂ���j
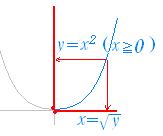
�@�t�̑Ή� y �� x ����܂邽�߂ɂ́C�P�� y �ɑ��đΉ����� x ���������܂�Ȃ���Ȃ�Ȃ����C���}�R�̂悤�ȏꍇ�C y �� x �́C�����P�� x �ɑΉ����Ă��Ȃ��D �@���̂悤�ɁC���̊� y=f(x) �Łu�قȂ�Q�ȏ�� x �̒l���P�� y �ɑΉ����Ă���ƁC�t�����̑Ή��������P�ɒ�߂��Ȃ��D�v �t�������݂��Ȃ��� �@���̐}�R�̊� y=x2 �ł� �@�}�S�ɂ��Ă����l 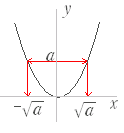 �}�S �}�S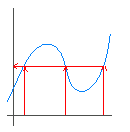 �@����ɑ��āC���}�T y=x2�@�i x��0 �j�ł́C�P�������̋�Ԃ������`��Ƃ��Ă���̂ŁCy��0 �̒l�ɑ��āC�Ή����� x �̒l�������P��܂�̂ŁC�t�������݂���D
�}�T
|
|
�@���̊��S�̂������Ƒ����̋�ԁC�����̋�Ԃ������ċt������`�ł��Ȃ��Ƃ��ł��C�P�������i�܂��͒P�������j�̋�Ԃ������`��ɂ���Ƌt������`�ł���D �@���̐}�U�ł́Cy=(x−2)2+1�@�i x��2 �j�ɑ��āC�t�������߂���D �@y=(x−2)2+1�@�i x��2 , y��1 �j �@(x−2)2=y−1�@�i x��2 , y��1 �j �@x−2=�@�i x��2 , y��1�C �y�d�v�z�@x−2��0 �������j �@x=+2�@�i x��2 , y��1 �j ���������ւ���� �@y=+2�@�i x��1 , y��2 �j  �@x−2=−�@�i x��2 , y��1�C �y�d�v�z�@x−2��0 �������j �̕��������ւ��� y=−+2�@�i x��1 , y��2 �j |
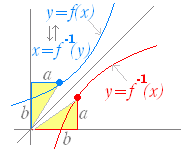
| ���@�t���̃O���t �@�� y=f(x) �̃O���t�Ƃ��̋t�� y=f −1(x) �̃O���t�Ƃ́C���� y=x �Ɋւ��đΏ̂ɂȂ�D
�i����jy=f(x) �� x=f −1(y) �Ƃ� x , y �̊W���Ƃ��Ă͓������̂ŁC��������ւ��������̂��̂Ȃ̂ŁC�_ (a , b) �� y=f(x) ��ɂ���Cx=f −1(y) ��ɂ�����D�i b=f(a) �� a=f −1(b) �j �@�����ŁC���� x , y �����ւ���Ǝ��}�̂悤�ɏc��������ւ�邩��C���� y=x �Ɋւ��đΏ̂ȓ_�Ɉړ�����D �@���Ȃ킿�C�_ (a , b) �� x=f −1(y) ��ɂ���Ca=f −1(b) �����藧���C�_ (b , a) �� y=f −1(x) ��ɂ���D |
 |
|
�@�� y=f(x) �Ƃ��̋t������������ƁC�P���� I(x)=x �ɂȂ�D���Ȃ킿�C
���@�P���� I(x)=x �Ƃ́C�ǂ�� x �̒l�ɑ��Ă��C����Ɠ����l���Ƃ���ŁC�ȒP�Ɍ����� y=x �̊��̂��ƁD
 f −1=I f −1=If −1  f=I f=I
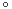 g=I g=Ig 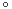 f=I f=I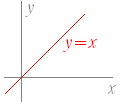 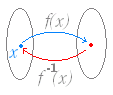 ���Ƌt������������ƌ��ɖ߂� |
| ���@�� f(x)=ex �̋t���� f −1(x)=log x f 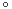 f −1=elog x=x f −1=elog x=xf −1 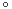 f=log (ex)=x f=log (ex)=x���@�� f(x)=x2 ( x��0 , y��0 ) �̋t���� f −1(x)= ( x��0 , y��0 ) f 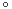 f −1=()2=x f −1=()2=xf −1 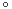 f= =x f= =x
����@�� f(x)= �̋t���� f(x) �ƈ�v����悤�ɒ萔 a �̒l���߂�D �i���āj �@f 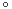 f=I ���K�v�\�������ƂȂ邩��C f=I ���K�v�\�������ƂȂ邩��Cf 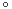 f====x ��� f====x ���a+1=0 �� a=−1 …�i���j |
|
���P�@�m��{�̃`�F�b�N�n �@���̊��̋t�������߂�D�i���̑I��������I�ׁD�j�@ �@ |
| ���Q�@�m�͖���背�x���n |
|
�y�ޑ�Ɠ��z �@���̊��̋t�������߁C���̒�`��C�l����q�ׂ�D
(1)
�i�j�@�u���̒�`�悪��������Ă��Ȃ��Ƃ��́C���̊�����`�ł���ł��L���͈͂��l���C�Ή�����l���l��Ƃ���v����C ���̊��̒�`��� �� �i�T�j�̕ϐ� ���������āC�t���� 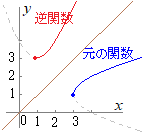 |
|
(2)
�i�j�@�u���̒�`�悪��������Ă��Ȃ��Ƃ��́C���̊�����`�ł���ł��L���͈͂��l���C�Ή�����l���l��Ƃ���v����C ���̊��̒�`��� �� �i�T�j�̕ϐ� ���������āC�t���� 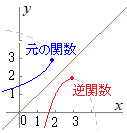 |
|
(3)
�i�j�@���̊��̒�`��� �� �ϐ� ���������āC�t����  |
|
(4)
�i�j�@���̊��̒�`��� �� �ϐ� ���������āC�t���� 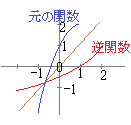 |
|
(5)
�i�j�@���̊��̒�`��� �� �ϐ� ���������āC�t����  |
|
(6)
�i�j�@���̊��̒�`��� �� �ϐ� ���������āC�t���� 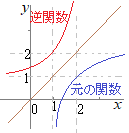 |
|
�m���n���O��PC�ł������ꂽ�ꍇ�́C�����]���ŃX�}�z�łɗ��Ă��܂��̂ŁC�u���E�U�́m�߂�L�[�n�ł͖߂�܂���i���X����ɂȂ�j�D���L�̃����N���g���ă��j���[�ɖ߂��Ă��������D
|
|
���m�ʂ̕ł���̎���ɑ���n[�t���ɂ��ā^17.8.15�n
����������
���m�ʂ̕ł���̎���ɑ���n[�t���ɂ��ā^16.12.8�n
�����m��ҁn�F�A�����肪�Ƃ��D ��{�̃`�F�b�N�̂Q��ڂʼn̔z�u�������Ǝv���܂��B
��2����I�����(3)��I�̂Ɂc
���m�ʂ̕ł���̎���ɑ���n[�t���ɂ��ā^16.10.13�n
�����m��ҁn�F�A�����肪�Ƃ��D��̈Í��̂悤�Ȋ��z����ǂ���̂ɂƂĂ����Ԃ�������܂����D�ǎ҂��u��{�̃`�F�b�N�̂Q��ڂʼn̔z�u�������Ǝv���܂��B�v�Əq�ׂĂ��邱�Ƃ���uEdge�Ƃ����u���E�U���g������C�ق��̃u���E�U�ƑS���قȂ�z�u�ɂȂ邱�Ƃ�����v�Ƃ����Ӗ����ƕ������āC�悤�₭�����ł��܂����D�˃u���E�U�Ȃǂ̏��������Ă��������D �e�X�g�O�ɂ��̃y�[�W�����Ă����̂ł����A��ς킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D |