← PC用は別頁
|
>のような分数不等式を解くときに,
分母のx−2は正とは限らないから,分母をそのまま払う訳にはいかない. このような分数不等式を解く方法として
(A) xの値に応じて場合分けして分母を払い,2次方程式に直して解く方法
の3つを紹介する.各自で解くときにはこれらのうちのどの方法でもよい.
(B) 通分だけで変形していく方法 (C) グラフを用いて解く方法
【例】
分数不等式>の解き方(A)
x<2とx>2の2つの場合に分けて解きます.左辺の分数関数はx=2のときに定義されませんので,x=2の場合を考える必要はありません.
(1) x<2のとき
両辺に2(x−2)<0を掛けて分母を払うと
(2) x>2のとき
2(x−4)<(x−2)(4−x) 2x−8<−x2+6x−8 x2−4x<0 x(x−4)<0 0<x<4 x<2の範囲で考えているから,0<x<2
両辺に2(x−2)>0を掛けて分母を払うと
(1)(2)から0<x<2, 4<x…(答)2(x−4)>(x−2)(4−x) 2x−8>−x2+6x−8 x2−4x>0 x(x−4)>0 x<0, 4<x x>2の範囲で考えているから,4<x
【Aの方法のまとめ】
分母を払って解くときは,分母が正になるか負になるかxの値に応じて分類して払わなければならない.
【例】
分数不等式>の解き方(C)
グラフが描ける場合は,交点の座標を「方程式」から求めて上下を見るだけでよい.方程式を解くときは不等式のときのように向きを考える必要がない点が長所です.
図1のように2つのグラフy=と
y=を描いておきます.図1 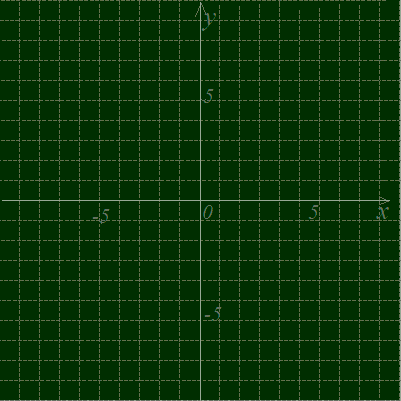
= x≠2のとき,分母を払って
2(x−4)=(x−2)(4−x)
図1において黄色のグラフy=は赤色のグラフ2x−8=−x2+6x−8 x2−4x=0 x(x−4)=0 x=0, 4 y=よりも上側にあるようなxの値の範囲を求めると, 0<x<2, 4<x…(答)
x=2の点では,一方の関数y=が定義
参考されていないので,大きいも小さいもなく,x=2の点は不等式の解に入りません. ○ 問題が<となっていれば,x<0, 2<x<4 が解となります. ○ 問題が≧となっていれば,0≦x<2, 4≦x が解となります. ○ 問題が≦となっていれば,x≦0, 2<x≦4 が解となります.
【Cの方法のまとめ】
左辺と右辺のグラフを描く(手書きのときは「そこそこの詳しさ」でよい.コンピュータで描くのとは違い細かいところまでは描けないが,漸近線や主な格子点(x座標もy座標も整数となる点)は押さえておく). 方程式から求めた解を見て上下を考える. |
|
【例】
分数不等式>の解き方(B)
(A)の分母を払う方法では,場合分けするために答案が冗長になりますが,こちらは場合分けせずに分数としての通分だけで変形していく方法です.
>
−>0 >0 >0 >0 >0 …(*) 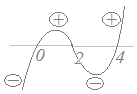 ここで両辺に2(x−2)2>0を掛けても不等号の向きは変わらないから
ここで両辺に2(x−2)2>0を掛けても不等号の向きは変わらないからx(x−4)(x−2)>0 …(**)(図参照) 0<x<2, 4<x…(答)
※ (*)(**)の変形について違和感を感じる人がいるかもしれませんので,補足説明
一般に…(*1)のような分数と2·3·4·5…(*2)のような 整数の「値」は等しくありませんが,それらの「符号」は同じです.(*1)に22·32(>0)を掛けると(*2)になるからです. 同様にして,…(*3)と(−2)·3·4·5…(*4)の 値は異なりますが,符号は同じです. ところで,不等式(*)を解くには,この不等式の左辺の「符号が正」となるようなxの値の範囲を求めればよく,この不等式の左辺が0.5だったらダメで,1.5ならよいなどという式の値を尋ねているのではありません. そこで,>0…(*)を解く代わりに,その両辺に 2(x−2)2(>0)を掛けたもの x(x−4)(x−2)>0…(**)を解くと,(*)と(**)の「符号」は等しくなります.
2(x−2)を掛けるのではありません.→これでは分母を払うのと同じでx(x−4)>0となって,そのような変形は分母が正とは限らないから,つねに正しい訳ではありません.
そうではなく分母の2乗22·32を掛けると,この式はつねに正で1枚は約分で消えて1枚が分子に掛けられるので,2x(x−4)(x−2)>0になるということです.(2は符号に関係ないから取り除いてもよい.) 一般に,>0 のような分数不等式は両辺に{f(x)g(x)}2を掛けて f(x)g(x)s(x)t(x)>0と変形して解くことができます. ただし,≧0の場合は f(x)g(x)s(x)t(x)≧0かつf(x)≠0, g(x)≠0です. (元の分数不等式において,分子が0になるのはよいが,分母が0になってはいけないから.)
【Bの方法のまとめ】
>0 ←→f(x)g(x)s(x)t(x)>0 <0 ←→f(x)g(x)s(x)t(x)<0 ≧0 ←→f(x)g(x)s(x)t(x)≧0, f(x)g(x)≠0 ≦0 ←→f(x)g(x)s(x)t(x)≦0, f(x)g(x)≠0 |
|
[第1問 / 全4問]
【問題】 次の不等式を解いてください. (暗算ではできませんので各自で計算用紙を使ってください.答が分数になるときは 2/3 のように書くものとし,負の分数になるときは −2/3 のように書くものとします.) 
|
|
|
|
■[個別の頁からの質問に対する回答][分数不等式の解き方について/18.6.22]
コメント失礼しますm(__)m
下の4つの問題の最初の第1番目の問題で誤りがあります。解答の2行目から3行目にかけて、分子の4x+1が4x+2になっています。
■[個別の頁からの質問に対する回答][分数不等式の解き方について/17.6.4]
=>[作者]:連絡ありがとう.訂正しました. 例えば,分子2 分母x-1 < x の場合はどうなりますか
■[個別の頁からの質問に対する回答][分数不等式の解き方について/16.8.15]
=>[作者]:連絡ありがとう.以下,質問が (A)の場合分けして分母を払う方法では,次のような答案になります. 1) x>1のとき
2<x(x−1)
2) x<1のとき(x=1のときという場合分けは不要であることに注意.分母が0になるから,成り立つはずがないから)x2−x−2>0 (x−2)(x+1)>0 x<−1, x>2 x>1の場合だから,x>2
2>x(x−1)
以上をまとめると,−1<x<1, x>2…(答)x2−x−2<0 (x−2)(x+1)<0 −1<x<2 x<1の場合だから,−1<x<1 (B)の通分だけで行う方法では,次のような答案になります. 両辺に 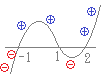
左図より,−1<x<1, x>2…(答) (C)のグラフを描く方法では,次のような答案になります. 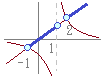 方程式に書き換えて交点のx座標を求めておく.
方程式に書き換えて交点のx座標を求めておく.左図より,y=xの方が上にあるのは,−1<x<1, x>2…(答) よかった
=>[作者]:連絡ありがとう.その頁では「画面上でグラフを描く」ために,筆者もそれなりに苦労したかもしれない. |