【センター試験 2006年度:数学I・A(本試験) 第1問[2]】
aは実数とし,bは0でない実数とする.aとbに関する条件p, q, rを次のように定める.
p:a, bはともに有理数である
(1) 次のスに当てはまるものを,下の0~3のうちから一つ選べ.q:a+b, abはともに有理数である r: 条件pの否定——pはスである. 0「a, bはともに有理数である」 1「a, bはともに無理数である」 2「a, bの少なくとも一方は有理数である」 3「a, bの少なくとも一方は無理数である」 (2) 次のセに当てはまるものを,下の0~3のうちから一つ選べ. 条件「qかつr」は条件pが成り立つためのセ. 0必要十分条件である 1必要条件であるが十分条件ではない 2十分条件であるが必要条件ではない 3必要条件でも十分条件でもない (3) 次の0~7のうち,正しいものはソである. 0「p⇒q」は真,「p⇒q」の逆は真,「p⇒q」の対偶は真である. 1「p⇒q」は真,「p⇒q」の逆は真,「p⇒q」の対偶は偽である. 2「p⇒q」は真,「p⇒q」の逆は偽,「p⇒q」の対偶は真である. 3「p⇒q」は真,「p⇒q」の逆は偽,「p⇒q」の対偶は偽である. 4「p⇒q」は偽,「p⇒q」の逆は真,「p⇒q」の対偶は真である. 5「p⇒q」は偽,「p⇒q」の逆は真,「p⇒q」の対偶は偽である. 6「p⇒q」は偽,「p⇒q」の逆は偽,「p⇒q」の対偶は真である. 7「p⇒q」は偽,「p⇒q」の逆は偽,「p⇒q」の対偶は偽である. |
現在地と前後の項目 集合の要素/集合の表わし方/部分集合,包含関係/共通部分と和集合/補集合/共通部分,和集合,補集合(練習問題)/ド・モルガンの法則/集合(楽しく入門,初歩から)/オイラー図/要素を用いた証明/必要・十分条件(等式)/必要・十分条件(不等式)/必要・十分条件(反例)/必要・十分条件入試問題1/必要・十分条件入試問題2/集合,条件.センター問題(2013~)/p→qの真偽/逆,裏,対偶/対偶証明法と背理法/背理法の入試問題/ スHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G セHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ソHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2007年度:数学I・A(本試験) 第1問[2]】
集合A, Bを A={ n | nは10で割り切れる自然数 } B={ n | nは4で割り切れる自然数 } とする. (1) 次のカとキに当てはまるものを,次の0~3のうちから一つずつ選べ.
自然数nがAに属することは,nが2で割り切れるためのカ.
自然数nがBに属することは,nが20で割り切れるためのキ.
0必要十分条件である1必要条件であるが,十分条件でない 2十分条件であるが,必要条件でない 3必要条件でも十分条件でもない (2) 次のク~コに当てはまるものを,下の0~7のうちから一つずつ選べ. C={ n | nは10と4のいずれでも割り切れる自然数 } D={ n | nは10でも4でも割り切れない自然数 } E={ n | nは20で割り切れない自然数 } とする.自然数全体の集合を全体集合とし,その部分集合Gの補集合を——Gで表すとき C=ク,D=ケ,E=コ である. 0A∪B 1A∪——B 2——A∪B 3——————A∪B 4A∩B 5A∩ ——B 6——A∩B 7——————A∩B |
カHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G キHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G クHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2008年度:数学I・A(本試験) 第1問[2]】
次のケ~シに当てはまるものを,下の0~3のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい. 自然数m, nについて,条件p, q, rを次のように定める.
p:m+nは2で割り切れる
また,条件pの否定を ——p ,条件rの否定を ——r で表す.このときq:nは4で割り切れる r:mは2で割り切れ,かつnは4で割り切れる
pはrであるためのケ.
0必要十分条件である——p は ——r であるためのコ. 「pかつq」はrであるためのサ. 「pまたはq」はrであるためのシ. 1必要条件であるが,十分条件でない 2十分条件であるが,必要条件でない 3必要条件でも十分条件でもない |
ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G サHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G シHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2009年度:数学I・A(本試験) 第1問[2]】
実数aに関する条件p, q, rを次のように定める.
p:a2≧2a+8
(1) 次のクに当てはまるものを,下の0~3のうちから一つ選べ.q:a≦−2またはa≧4 r:a≧5
qはpであるためのク
(2) 条件qの否定を ——q ,条件rの否定を ——rで表す.0必要十分条件である 1必要条件であるが,十分条件でない 2十分条件であるが,必要条件でない 3必要条件でも十分条件でもない
次のケ,コに当てはまるものを,下の0~3のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい.
命題「pならばケ」は真である.
0qかつ——r命題「コならばp」は真である. 1qまたは——r 2——qかつ——r 3——qまたは——r |
クHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2010年度:数学I・A(本試験) 第1問[2]】
次のケ~サに当てはまるものを,下の0~3のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい.また,シに当てはまるものを,下の4~7のうちから一つ選べ.
自然数nに関する条件p, q, r, sを次のように定める.
p:nは5で割ると1余る数である q:nは10で割ると1余る数である r:nは奇数である s:nは2より大きい素数である また,条件rの否定を ——r,条件sの否定を ——sで表す.このとき
「pかつr」はqであるためのケ.
45——rは——sであるためのコ. 「pかつs」は「qかつs」であるためのサ. 0必要十分条件である 1必要条件であるが,十分条件でない 2十分条件であるが,必要条件でない 3必要条件でも十分条件でもない 自然数全体の集合を全体集合Uとし,条件pを満たす自然数全体の集合をP,条件rを満たす自然数全体の集合をR,条件sを満たす自然数全体の集合をSとすると,P, R, Sの関係を表す図はシである. 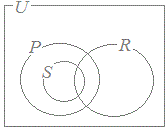 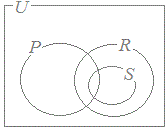 67 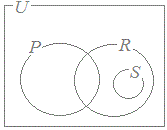 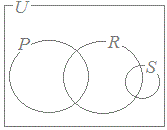 |
ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G サHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G シHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2011年度:数学I・A(追試験) 第1問[2]】
1から100までのすべての自然数の集合を全体集合Uとし,その部分集合A, B, Cを次のように定義する.
A={ x | xは偶数 }
(1) A, B, Cの関係を表す図は,次の0~3のうちセである.B={ x | xは3の倍数 } C={ x | xは4の倍数 } 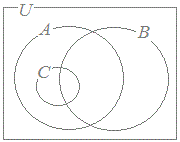 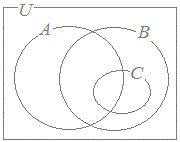 23 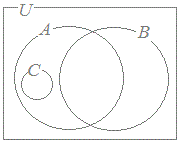 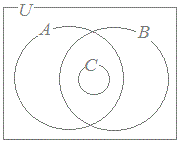
(2) Cの補集合を——Cで表す.また,xが集合Sの要素であることをx∈Sと表す.
x∈Cはx∈A∩Bであるためのソ.
x∈A∩——Cはx∈Aであるためのタ. x∈A∪Bは「x∈A∩——Cまたはx∈B」であるためのチ. x∈A∪Bは「x∈Aまたはx∈B∩——C」であるためのツ.
ソ~ツに当てはまるものを,次の0~3のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい.
0必要十分条件である
1必要条件であるが,十分条件ではない 2十分条件であるが,必要条件ではない 3必要条件でも十分条件でもない |
セHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ソHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G タHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G チHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ツHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2011年度:数学I・A(本試験) 第1問[2]】
実数a, bに関する条件p, qを次にように定める.
p:(a+b)2+(a−2b)2<5
q:|a+b|<1または|a−2b|<2
(1) 次の0~3のうち,命題「q⇒p」に対する反例になっているのはチである.
0a=0, b=0 1a=1, b=0 2a=0, b=1 3a=1, b=1
(2) 命題「p⇒q」の対偶は「ツ⇒テ」である.
ツ,テに当てはまるものを,次の0~7のうちから一つずつ選べ. 0|a+b|<1かつ|a−2b|<2 1(a+b)2+(a−2b)2<5 2|a+b|<1 または|a−2b|<2 3(a+b)2+(a−2b)2≦5 4|a+b|≧1かつ|a−2b|≧2 5(a+b)2+(a−2b)2>5 6|a+b|≧1または|a−2b|≧2 7(a+b)2+(a−2b)2≧5
(3) pはqであるためのト.
トに当てはまるものを,次の0~3のうちから一つ選べ.
0必要十分条件である
1必要条件であるが,十分条件ではない 2十分条件であるが,必要条件ではない 3必要条件でも十分条件でもない |
チHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ツHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G テHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G トHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2012年度:数学I・A(追試験) 第1問[2]】
m, nを整数とする.
次のク,コに当てはまるものを,下の0~5のうちから一つずつ選べ.また,次のケ,サに当てはまるものを,下の6~9のうちから一つずつ選べ.ただし,ケ,サには,同じものを繰り返し選んでよい.
(1) m, nに関する条件p, qを次のように定める.
p:m, nの少なくとも1つは3の倍数でない
q:m+n, m−nの少なくとも1つは3の倍数でない
pの否定——pはク.
pはqであるためのケ.
(2) m, nに関する条件r, sを次のように定める.
r:m, nの少なくとも1つは4の倍数でない
s:m+n, m−nの少なくとも1つは4の倍数でない
sの否定——sが成立するならば,コ.
rはsであるためのサ.
0m, nの少なくとも1つは3の倍数である
1m, nはともに3の倍数である 2m, nはともに3の倍数でない 3m, nはともに奇数である 4m, nはともに偶数である 5m, nのうち一方だけが偶数である
6必要十分条件である
7必要条件であるが,十分条件でない 8十分条件であるが,必要条件でない 9必要条件でも十分条件でもない |
クHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G サHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2012年度:数学I・A(本試験) 第1問[2]】 kを定数とする.自然数m, nに関する条件p, q, rを次のように定める.
p:m>kまたはn>k
(1) 次のクに当てはまるものを,下の0~3のうちから一つ選べ.q:mn>k2 r:mn>k
pの否定——pはクである.
0m>kまたはn>k
1m>kかつn>k 2m≦kかつn≦k 3m≦kまたはn≦k
(2) 次のケ~サに当てはまるものを,下の0~3のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい.
(i) k=1とする.
pはqであるためのケ.
(ii) k=2とする.
pはrであるためのコ.
pはqであるためのサ.
0必要十分条件である
1必要条件であるが,十分条件でない 2十分条件であるが,必要条件でない 3必要条件でも十分条件でもない |
クHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G サHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
【センター試験 2013年度:数学I・A(本試験) 第1問[2]】 三角形に関する条件p, q, rを次のように定める.
p:三つの内角がすべて異なる
条件pの否定を——pで表し,同様に——q, ——rはそれぞれ条件q, rの否定を表すものとする.q:直角三角形でない r:45°の内角は一つもない (1) 命題「r⇒(pまたはq)」の対偶は「ク⇒——r」である.
クに当てはまるものを,次の0~3のうちから一つ選べ.
0(pかつq)1(——pかつ——q)2(——pまたはq)3(——pまたは——q) (2) 次の0~4のうち,命題「(pまたはq)⇒r」に対する反例となっている三角形はケとコである.
ケとコに当てはまるものを,次の0~4のうちから一つずつ選べ.ただし,ケとコの解答の順序は問わない.
0直角二等辺三角形1内角が30°,45°,105°の三角形 2正三角形 3三辺の長さが3, 4, 5の三角形 4頂角が45°の二等辺三角形 (3) rは(pまたはq)であるためのサである.
サに当てはまるものを,次の0~3のうちから一つ選べ.
0必要十分条件である
1必要条件であるが,十分条件ではない 2十分条件であるが,必要条件ではない 3必要条件でも十分条件でもない |
クHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G
[2つ答えたときに採点]
ケHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G コHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G サHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |