← PC用は別頁
※高校数学Ⅲの「媒介変数表示・極座標」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　 が現在地です．
↓媒介変数表示1
↓同(2)
↓放物線の頂点・円の中心の軌跡
↓サイクロイド,アステロイド等
↓極座標
↓極方程式
↓同(2)-現在地
2次曲線の極方程式,媒介変数表示

== 極方程式2 ==
【極方程式とは】
　極座標(r, θ)を使って，曲線のグラフを
r=f(θ)
θ=g(r)
F(r, θ)=0
などの形で表したものを極方程式といいます．

【例１】
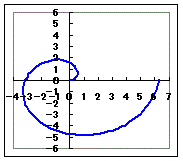
アルキメデスの渦巻線（アルキメデスの螺旋）
r=aθ（a>0, θ≧0）
（次のグラフは，a=1の場合，すなわちr=θのグラフです．）

（曲線の特徴）
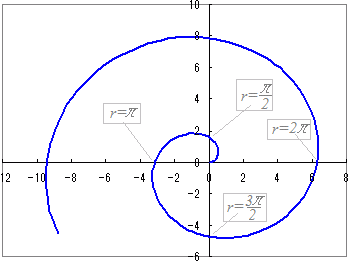
　この曲線は，θ≧0となるθの値に対して無限に成長していきます．特に，一周すると（θ=+2π）以前の周回のときとは異なる点を通りますので，θ=0, θ=2π, θ=4π, ...はそれぞれ異なる点となり，渦巻きのように成長します．
（手書きで概形［だいたいの形］を描く方法）
(1)　主な点の(r, θ)座標を計算して，点を描きます．
θ=0のときr=0
θ=.π2nのときr=.π2n
θ=πのときr=π
θ=.3π2nnのときr=.3π2nn
θ=2πのときr=2π
(2)　なるべく滑らかに点を結びます．（θ=.π6n, .π4n, .π3nなどと細かく分ければ，さらに滑らかに描けます．）
（Excelを使って，コンピュータでこのグラフを描く方法）

※　コンピュータでグラフを描くときの考え方のポイント
○　コンピュータの画面上では，無限に細かく点や線が描けるのではなく，それぞれの画面の解像度に応じて描ける点の数は決まっています．（横1600×縦900など）
　したがって，画面上に数学的に厳密に正確な曲線を描くことは，もともとできません．画面に描けるのは，点や折れ線です．
　そこで，例えば，θ=0からθ=3π=9.43...までの部分を描くとき，θの値として0.1ずつ増やして「折れ線をつなげば」十分正確な「曲線」が描けます．0から9.5までを0.1ずつ増やしていくには，96行のデータを用意すればよいことになります．（表題分が+１行あります）
○　Excelで用意されているグラフツールは(x, y)座標向けですので，極座標(r, θ)で求めた点を直交座標(x, y)に計算し直します．
○　*** ここがポイント ***
　数学的に厳密に正確な曲線の代わりに「折れ線」で代用するといっても，グラフツールのメニューで「折れ線」を選ぶのではなく「散布図」を選ぶことが重要です．･･･「折れ線グラフ」は，データとしてy座標だけ（１次元）が与えられたときに（xの増分が１ずつに決まっているときに）グラフを描くものです．これに対して，x座標もy座標も（２次元に）指定して点を打つときは「散布図」を選びます．
　散布図は上の左側の例のように(x,y)座標に応じた点を表示するものですが，オプションとしてテータポイントを線でつなぐことが選べるようになっています．（どの点からどの点に線を引くのかは，元のデータで並び方によります．元のデータで１番目になる点から２番目の点へ，２番目の点から３番目の点へ，...と線が引かれます．）
　このときに，「点」を目立たないように，「線」だけを生かしたいとき「データポイントを平滑線でつないだマーカーなしの散布図」を選びます．

A B C D
1 θ r x y
2 0 0 0 0
3 0.1 0.1 0.100 0.010
4 0.2 0.2 0.196 0.040
5 0.3 0.3 0.287 0.089
... ... ... ... ...
(1)　図のように，θ, r, x, yというタイトル［表題］を付けます．（なくてもグラフは描けますが，自分自身が間違わないようにするために，表題がある方がよい）
(2)　セルA2にθの初期値0を書き込み，A2からA97まで選択・反転表示させて，「編集メニュー」の「フィル→連続データの作成→増分値0.1」とすると，θの欄が埋まります．
(3)　この例ではr=θのグラフを描きたいので，セルB2に=A2と書きこみます．
(4)　直交座標に直す公式はx=r cosθ, y=r sinθなので，セルC2に=B2*cos(A2)，セルD2に=B2*sin(A2)と書き込み，セルB2～D2の３列を選択・反転表示させて，コピーし，セルB3からセルB97に貼り付けると，相対参照によりすべてのデータが準備できます．
(5) *** ここがポイント ***
　タイトル［表題］を除く(x,y)座標C2～D97までを選択・反転表示させ，グラフツールを使って「散布図」の「データポイントを平滑線でつないだマーカーなしの散布図」を選びます．

【例２】
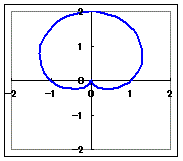
カージオイド（心臓形）
r=a(1+cosθ)（a>0）
（次のグラフは，a=1の場合，すなわちr=1+cosθのグラフです．）

（曲線の特徴）
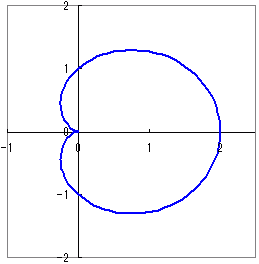
　cos(θ+2nπ)=cosθなので，１周すれば元に戻り，同じ曲線上をたどります．したがって，0≦θ<2πの値に対してグラフを描けば全部描けます．
　また，cos(−θ)=cosθだから（右に回っても左に回ってもrが等しくなるので）グラフは上下対称になります．（cos(π−θ)=cos(π+θ)だから上下対称だと考えてもよい．）
（手書きで概形［だいたいの形］を描く方法）
(1)　主な点の(r, θ)座標を計算して，点を描きます．
θ=0のときr=2
θ=.π6nのときr=1+..√3√ni2nn=1.87...
θ=.π4nのときr=1+..√2√ni2nn=1.70...
θ=.π3nのときr=1+.12n=1.5
θ=.π2nのときr=1
θ=.2π3nnのときr=1−.12n=0.5
θ=.3π4nnのときr=1−..√2√ni2nn=0.29...
θ=.5π6nnのときr=1−..√3√ni2nn=0.13...
θ=πのときr=0
(2)　なるべく滑らかに点を結び，π≦θ<2πについては上下対称に描きます．

（Excelを使って，コンピュータでこのグラフを描く方法）

【例１】と同様の考え方で，極座標(r, θ)で求めた点を直交座標(x, y)に計算し直し，「データポイントを平滑線でつないだマーカーなしの散布図」を選べばグラフが描けます．
(1)　0≦θ<2π=6.28...まで（0.1ずつ増加させるときは64個）の値を準備すればよい．
(2)　r=1+cosθだから，セルB2に=1+cos(A2)と記入し，これをコピーしてB65まで（式を）貼り付けるとよい．
(3)　x=r cosθ, y=r sinθとすることは【例１】と同じ．

【例３】
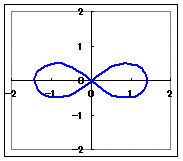
レムニスケイト（連珠形，双眼形）
r2=2a2cos2θ（a>0, cos2θ≧0）
⇔ r=a.√2cos2θ√nnnnnni（a>0, cos2θ≧0）
（次のグラフは，a=1の場合，すなわちr=.√2cos2θ√nnnnnniのグラフです．）

（曲線の特徴）
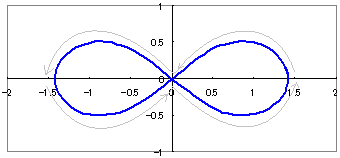
　cos2(−θ)=cos2θなので，上下対称です．
　また，cos2(.π2n−θ)=cos(π−2θ)=−cos2θ
　　　　cos2(.π2n+θ)=cos(π+2θ)=−cos2θ
だから，cos2(.π2n−θ)=cos2(.π2n+θ)になり，左右対称です．
　したがって，0≦θ≦.π2nの値に対してグラフを描いて，上下左右対称に折り返すと全部描けます．
　この範囲のうちで，0≦θ≦.π4nのときは，cos2θ≧0となり関数は定義されますが，.π4n<θ<.π2nのときは，cos2θ<0となり関数は定義されません．
（手書きで概形［だいたいの形］を描く方法）
(1)　主な点の(r, θ)座標を計算して，点を描きます．
θ=0のときr=.√2cos0√nnnnni=.√2√ni≒1.41
θ=.π6nのときr=.√2cos.π3n√nnnnni=1
θ=.π4nのときr=.√2cos.π2n√nnnnni=0
(2)　なるべく滑らかに点を結び，上下左右対称に折り返します．

（Excelを使って，コンピュータでこのグラフを描く方法）

【例１】と同様の考え方で，極座標(r, θ)で求めた点を直交座標(x, y)に計算し直し，「データポイントを平滑線でつないだマーカーなしの散布図」を選べばグラフが描けます．
(1)　cos2θ≧0のときだけ，r=.√2cos2θ√nnnnnniだから，セルB2に=IF(cos(2*A2)>=0, SQRT(2*cos(2*A2)))と記入し，これをコピーして（式を）貼り付けるとよい．
(3)　x=r cosθ, y=r sinθとすることは【例１】と同じ．

※高校生が以下の結果を「覚える」必要はないでしょう．なんとなくパラパラと見ておいて，「作り方がわかる」，「だいたいの規則性がわかる」というくらいのことでよいと思います．
【例４】 正葉線（正葉曲線，バラ曲線）…日本では木の葉に見え，西洋ではバラの花びらに見えるということらしい．
（以下については，a=1の場合について，グラフの概形のみ示します．）
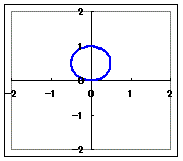
(1)r=a cosθ（a>0）…１枚の葉：円になります．

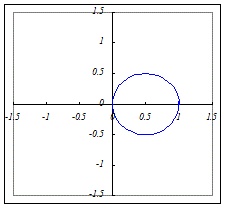(2)r=a cos(3θ)（a>0）…３枚の葉になります．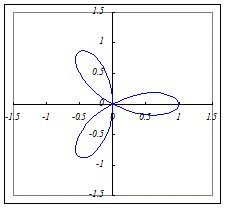

(3)r=a cos(5θ)（a>0）…５枚の葉になります．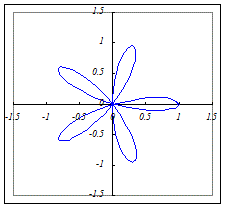
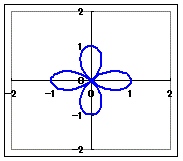
⇒ 一般に，r=a cos(nθ)（a>0, nは奇数）は，ｎ枚の葉になります．

(4)r=a cos(2θ)（a>0）…４枚の葉になります．（２枚ではありません）

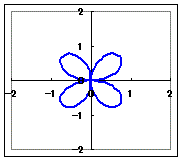
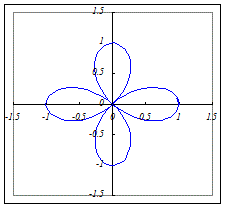(5)r=a cos(4θ)（a>0）…８枚の葉になります．（４枚ではありません．）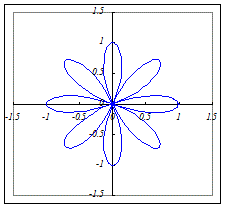

(6)r=a cos(6θ)（a>0）…12枚の葉になります．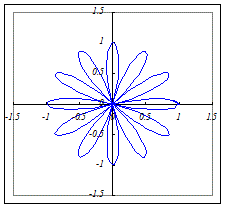
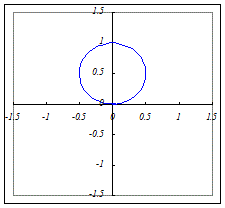
⇒ 一般に，r=a cos(nθ)（a>0, nは偶数）は，２ｎ枚の葉になります．
(1)r=a sinθ（a>0）…１枚の葉：円になります．
a sinθ=a cos(.π2n−θ)=a cos(θ−.π2n)だから，左のグラフを+.π2nだけ回転したものになります．

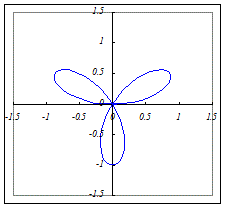
(2)r=a sin(3θ)（a>0）…３枚の葉になります．
a sin(3θ)=a cos(.π2n−3θ)=a cos(3θ−.π2n)=a cos(3(θ−.π6n))だから，左のグラフを+.π6nだけ回転したものになります．

(3)r=a sin(5θ)（a>0）…５枚の葉になります．
a sin(5θ)=a cos(.π2n−5θ)=a cos(5θ−.π2n)=a cos(5(θ−.π10nn))だから，左のグラフを+.π10nnだけ回転したものになります．
⇒ 一般に，r=a sin(nθ)（a>0, nは奇数）は，ｎ枚の葉になります．

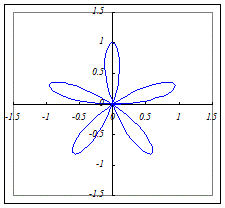
(4)r=a sin(2θ)（a>0）…４枚の葉になります．
a sin(2θ)=a cos(.π2n−2θ)=a cos(2θ−.π2n)=a cos(2(θ−.π4n))だから，左のグラフを+.π4nだけ回転したものになります．

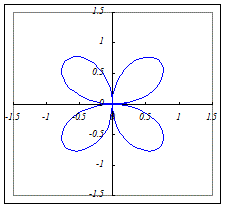(5)r=a sin(4θ)（a>0）…８枚の葉になります．
a sin(4θ)=a cos(.π2n−4θ)=a cos(4θ−.π2n)=a cos(4(θ−.π8n))だから，左のグラフを+.π8nだけ回転したものになります．

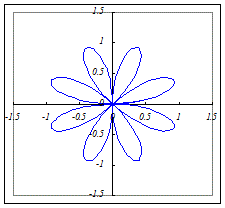(6)r=a sin(6θ)（a>0）…12枚の葉になります．
a sin(6θ)=a cos(.π2n−6θ)=a cos(6θ−.π2n)=a cos(6(θ−.π12nn))だから，左のグラフを+.π12nnだけ回転したものになります．
⇒ 一般に，r=a sin(nθ)（a>0, nは偶数）は，２ｎ枚の葉になります．

【問題】次の極方程式に対応するグラフを下から選んでください．
○はじめに極方程式を選び，続いてグラフを選んでください．
○間違ったときは，極方程式を選び直してください．
○間違った後にHELPで表示されるのは方程式に対する解説です．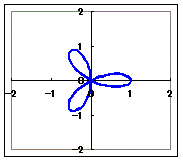






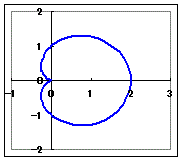
r=θ(θ≧0)



［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．
...（携帯版）メニューに戻る

...（PC版）メニューに戻る
■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります