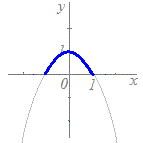|
x, y座標がそれぞれ第3の変数tを用いて
【媒介変数表示で表される曲線・直線の調べ方】
(A) t=0,1,2などいくつかの値に対応する点を調べてみる.
この方法は,原始的なもので,すべてのtの値に対して調べている訳ではないので,軽く見られがちですが,2,3の値について調べてみると重要な傾向が分かります.
(B) 媒介変数を消去してx, yの方程式に直す.このとき,媒介変数の値の範囲に制限があるときは,消去するときにx, yの範囲として残す必要があります.…(B-1)
媒介変数tを消去するために,一方の式からtについて解いて,他方の式に代入するというのが良く用いられる方法ですが,必ずしもそうしなければならない訳ではなく,何らかの関係式を利用して消去できればよい.…(B-2)
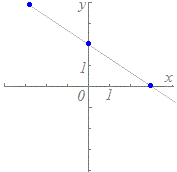
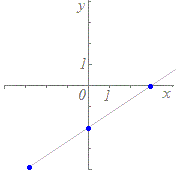
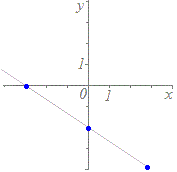
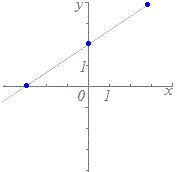
(A)の【例】
t=0のときx=1, y=−1 → 点(1, −1)を通る
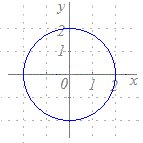
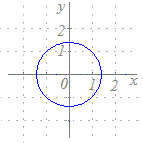
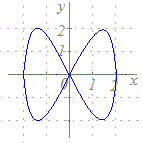
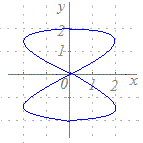
t=1のときx=3, y=2 → 点(3, 2)を通る t=2のときx=5, y=5 → 点(5, 5)を通る 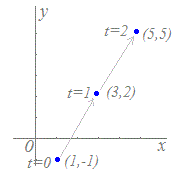 ※この方法は,数学的には原始的に見えますが,コンピュータを用いてグラフを描くときには,重宝します.次の媒介変数表示で表される図形(リサジュー曲線)
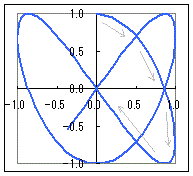 |
|||||||||||||||||||||||||||||||
|
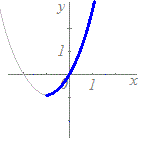
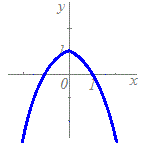
(B-1)の【例】
この例では,t≧0のときだけ関数が定義されるので,
x+1=≧0 すなわち, x≧−1 という条件が付きます. 求める曲線はtを消去してできるx, yの関係式 y=(x+1)2+1 の全部ではなく,そのうちのx≧−1の部分になります.
【重要】
tは消去されるが,tに付いていた条件は残さなければならない. t≧0の条件はx≧−1として引き継ぐ.  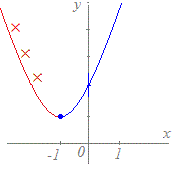
(B-2)の【例】
この例では,tについて解けない(無理やり解く方法:t=cos−1xもあるが,それは元の関数の逆関数を表す形式的な記号であまりうれしくない)が,三角関数の次の公式に代入すると
sin2t+cos2t=1 x, yが消去できます. x2+y2=1 このように,媒介変数を消去することにとって「tについて解いてから」という手続きは必ずしも必要なことではない. |