|
【例題1.1】
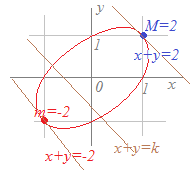
x+y=2のとき,xyの最大値を求めてください.
条件式が1次方程式のときは,その方程式を使って1つの文字yを消去して,1つの変数xの関数に直して考えるのが基本です.(xを消去してもよい)
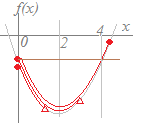
(解答)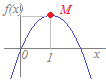 この参考図において,縦はyではなく,求める関数xyをxの関数として表したものであることに注意 xy=x(2−x)=−x2+2x =−{x2−2x}=−{(x−1)2−1} =−(x−1)2+1 右図のような2次関数になり,x=1(このときy=1)のとき最大値1になる.
【例題1.2】
x+2y=3のとき,2x2+y2の最小値を求めてください.
条件式の方程式を使って1文字を消去しますが,yを消去すると初めから分数が登場します.
(解答)この形ならxを消去する方が有利でしょう 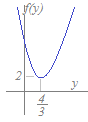 この参考図において,縦はyではなく,求める関数2x2+y2をyの関数として表したものであることに注意 2x2+y2=2(3−2y)2+y2 =2(4y2−12y+9)+y2 =9y2−24y+18 ゆえに |
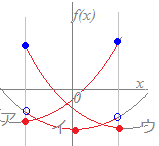
【問題1】 選択肢の中から正しい答を選んでください.(クリックする)
y=1−xを代入すると
2x2−3y2=2x2−3(1−x)2 =2x2−3(x2−2x+1) =−x2+6x−3 =−(x2−6x)−3 =−{(x−3)2−9}−3 =−(x−3)2+9−3 =−(x−3)2+6 x=3, y=−2のとき最大値6をとる |
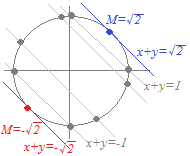 2次方程式(*)が実数解をもつための条件は
2次方程式(*)が実数解をもつための条件は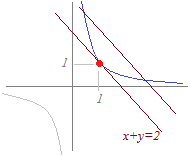 2次方程式(*)が実数解をもつための条件は
2次方程式(*)が実数解をもつための条件は