|
■解説・・・指数不等式の解き方
[要点]
下のグラフから分かるように, (1) a>1のとき y=ax は増加関数だから ※(2)で関数の大小と指数の大小が逆になるところが要注意です。 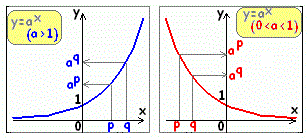 ●(1)の例
●(2)の例
|
|
■解説・・・指数不等式の解き方
[要点]
下のグラフから分かるように, (1) a>1のとき y=ax は増加関数だから ※(2)で関数の大小と指数の大小が逆になるところが要注意です。  ●(1)の例
●(2)の例
|
|
■問題・・・次の不等式を解きなさい。
1
|
| ◆ヒント1◆◆ヒント2◆◆ヒント3◆◆ヒント4◆
(32)x+1>
34
==>
32x+2 > 34
==>
底3は1より大だから 2x+2 > 4
==>
2x > 2
|
|
2
|
| ◆ヒント1◆◆ヒント2◆
==>
底
|
|
3
|
| ◆ヒント1◆◆ヒント2◆◆ヒント3◆◆ヒント4◆
(32)x+3≦(33)x-1
==> 32x+6≦33x-3
==> 底3は1より大きいから 2x+6≦3x-3
==> -x≦-9
|
|
4
|
| ◆ヒント1◆◆ヒント2◆
==> 底
|
|
5--2005年度 神奈川大(理・工学部)入試問題の引用--
不等式 22x-2x+1≦8 を満たすxの値の範囲は[ ]である。 |
| ◆ヒント1◆◆ヒント2◆◆ヒント3◆◆ヒント4◆
2x=t (>0)・・(1)とおくと t2-2t≦8
==> (t-4)(t+2)≦0
==> -2≦t≦4・・(2)
==> (1)(2)より (0<) t≦4すなわち2x≦22
|
|
6 --2000年度 関西大学(経済学部)入試問題の引用--
不等式 |
◆ヒント1◆◆ヒント2◆◆ヒント3◆◆ヒント4◆
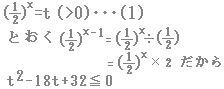 ==> (t-16)(t-2)≦0
==> 2≦t≦16 すなわち
==> 底
|
|
|