|
指数(累乗)は底を何回掛けるかを表しています. 次の式でaを底といい,nを指数といいます. an=a×a×a×… (←n 回)
例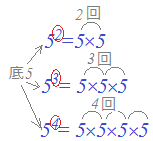 •指数法則: am×an=am+n …(3)
例a2×a3=(a×a)×(a×a×a)=a×a×a×a×a=a5 ∴a2×a3=a2+3
am÷an=
=am−n …(4)
例a5÷a3==a2 ∴a5÷a3=a5−3
(am)n=amn …(5)
例(a2)3=a2×a2×a2=a6 ∴(a2)3=a2×3
(ab)n=anbn …(6)
例(ab)3=ab×ab×ab=a3b3 ∴(ab)3=a3b3 この頁では「負の指数と0の指数」を定義します.
■負の指数,0の指数の定義
(1)(2)←解説a≠0, nを正の整数とするとき a−n= …(1) a0=1 …(2) 指数が1ずつ増加するとき,式の値は底aの値だけ掛けたものになります. 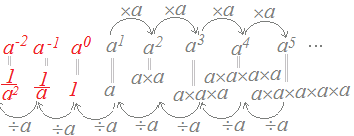 このようにして a0=a1÷a=1, a−1=a0÷a=, a−2=a−1÷a=, a−3=a−2÷a=, … a−n=, (1)←別の解説 m<nのとき,次の式には負の指数が登場します.
am÷an==am−n
例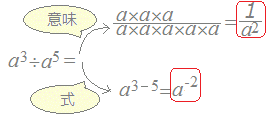 このようにして式a−2の意味をと決めると, am÷an=am−nの計算で「負の指数」が登場してもよいようになります. 一般に a−n=と決めればよいことになります. (2)←別の解説 m=nのとき,次の式には0の指数が登場します.
an÷an==a0
例 このようにしてa0の意味を1と決めると,am÷an=am−nの計算で「0の指数」が登場してもよいようになります. |
|
注意!・・・見かけだけで「うっかりミス」をする生徒が多い
•a−nはaと等しいのではない.に等しい. •a0は0に等しいのではない.1に等しい. |
|
上の解説では指数法則(4)がm<nやm=nのときにも成り立つように負の指数,0の指数を定義しましたが,
a≠0, n, m は任意の整数(正,負,0)とするとき, a−n= , a0=1と定義すれば ”指数法則” (3)(4)(5)(6)がそのまま使えるようになります. 以下の例において,途中経過は青で示したように負の指数を使って書くのがよく,最終答案は赤で示したように書くとよい.これは,高校生のうちでは意味が分からないまま負の指数や0の指数を使って答だけが合っているというのを防ぐためだと考えればよい.(高卒以上では負の指数のまま答にすることが普通に行われる.) (3)→例
負の指数のまま計算すると a−2a5=a−2+5=a3 定義に従って負の指数を分数に戻すと a−2a5=a5=a3 これらは等しいから,青で示したように単に指数の足し算をすればよい. (3)→例
負の指数のまま計算すると
a−2a−3=a−2−3=a−5 定義に従って負の指数を分数に戻してから計算すると a−2a−3== これらは等しいから,最後の結果だけ赤で示したように書き直せばよい. a−2a−3=a−2−3=a−5= (4)→例
負の指数のまま計算すると
a−5÷a−3=a−5−(−3)=a−2 定義に従って負の指数を分数に戻してから計算すると a−5÷a−3=÷=×a3= これらは等しいから,最後の結果だけ赤で示したように書き直せばよい. a−5÷a−3=a−5−(−3)=a−2= |
|
(5)→例
負の指数のまま計算すると
(a−2)3=a−2×3=a−6 定義に従って負の指数を分数に戻してから計算すると (a−2)3=()3= これらは等しいから,最後の結果だけ赤で示したように書き直せばよい. (a−2)3=a−2×3=a−6= (5)→例
負の指数のまま計算すると
(a−2)−3=a−2×(−3)=a6 定義に従って負の指数を分数に戻してから計算すると (6)→例
負の指数のまま計算すると
(a−2b3)−4=a−2×(−4)b3×(−4)=a8b−12 定義に従って負の指数を分数に戻してから計算すると これらは等しいから,最後の結果だけ赤で示したように書き直せばよい. (a−2b3)−4=a−2×(−4)b3×(−4)=a8b−12 = |
|
問題次の式と等しいものを選びなさい. 0 1 2 4 8 2 2 2 |
|
2−3== |
|
0 1 2 4 8 2 2 2 |
|
20=1 |
|
0 1 2 4 8 2 2 2 |
|
()−3=(2−1)−3=23=8 |
|
0 1 a a2 a3 a a |
|
a−2= |
|
0 1 a a2 a3 a a |
|
a0=1 |
|
0 1 a a2 a4 a6 a8 a a a a |
|
a2a−4=a2+(−4)=a−2= |
|
0 1 a a2 a4 a6 a8 a a a a |
|
a2÷a−4=a2−(−4)=a6 |
|
0 1 a a2 a4 a6 a8 a a a a |
|
(a2)−4=a2×(−4)=a−8= |
|
0 1 a a2 a4 a6 a8 a a a a |
|
(a−2)−4=a−2×(−4)=a8 |
|
0 1 a a2 a4 a6 a8 a a a a |
|
a2÷a−2×a4=a2−(−2)+4=a8 |
|
0 1 a a2 a4 a6 a8 a a a a |
|
(a2)−4÷(a−3)2=a−8÷a−6=a−8−(−6)=a−2= |
|
0 1 8 9 |
|
(3−2×2)−1÷(3×2−1)−2=322−1÷3−222 =32−(−2)2−1−2=342−3= |
|
■[個別の頁からの質問に対する回答][負の指数について/17.3.25]
いい教材を作っていただきありがとうございます
■[個別の頁からの質問に対する回答][負の指数について/16.12.8]
=>[作者]:連絡ありがとう. 問8?
=>[作者]:連絡ありがとう.問8がどうかしましたか?選択肢のうちのいずれかを選んでもらうとhelpが出ますので,それを読んでください. |