|
○ 関数 F(x) を微分すると f(x) になるとき, すなわち, F(x)=f(x) ⇔ f(x)dx=F(x)+C のとき,F(x) を f(x) の(1つの)原始関数,F(x)+C を f(x) の不定積分という. 例 (x2)=2x ⇔ 2xdx=x2+C だから x2 を 2x の原始関数,x2+C を 2x の不定積分という. ○ 関数 f(x) の1つの原始関数を F(x) とするとき,F(b)−F(a) の値を f(x) の a から b までの定積分といい, f(x)dx で表わす.すなわち, 実際の計算に当たっては, f(x) から F(x) を求めて,次に x=a , b を代入するために,
【要点】 定積分の定義
※ よくある間違いF(a)−F(b) ではなく F(b)−F(a) なので注意すること. 例1 2x dx=x2=22−12=3 |
注意 (x2+1)=2x (x2+2)=2x (x2+3)=2x だから,x2+1 , x2+2 , x2+3 , … も 2x の原始関数であり,2x の原始関数は1つではない. 定積分の計算には,そのうちどれか1つの原始関数を用いればよいが,計算が簡単なように C=0 となるものを用いる. すなわち, となり,どんな C の値を用いても差で消えるので,計算が最も簡単になる C=0 の場合を用いる.  [なぜ原始関数を使うのか,なぜ差なのか,そんなことをして何になるのか] [なぜ原始関数を使うのか,なぜ差なのか,そんなことをして何になるのか](教科書の項目として面積の項目は定積分の後に登場するが,)原始関数 F(x) は,関数 f(x) (>0) の下にできる図形の面積を表わし, 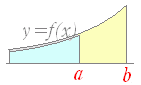 F(b)−F(a) で a≦x≦b の区間の面積を表わせるので,このように定義すると豊かな応用が広がってくるのである. F(b)−F(a) で a≦x≦b の区間の面積を表わせるので,このように定義すると豊かな応用が広がってくるのである.(b よりも左の面積)-(a よりも左の面積)=(a , b の間の面積) |
|
例2 右のように x の1つの原始関数は
x dx== −= 例3 右のように x2 の1つの原始関数は x2 dx== −= |
【不定積分の公式:復習】 xn の不定積分
xndx= +C ※ (xn+1)=(n+1)xn だから ( )=xn となる. |
| 問題1 次の定積分を求めよ.(やさしい) 初めに [ ? ] を1つ選び,続いて右の欄から解答を1つ選べ.正しければ解答が入り,間違っていればもとに戻る. |
|
| 問題2 次の定積分を求めよ.(空欄を埋めよ) |
(1)
(2x+1)dx=
x2
+x
= (4+2)−(1+1)=4
(2) (3x2+2x)dx= x3+x2 =(1+1)−0=2 (3) (x2−2x+2)dx= −x2+2x =(9−9+6)−(−1+2)= |
| ○ 多項式の積や累乗の定積分
【要点】 (I)(II)は不定積分と共通の性質.(III)は定積分だけの性質
(II)は,数学IIIで学ぶ「置換積分」を用いて証明できるが,数学IIではその結果を利用する.(ここでは証明略)(I) 多項式の積や累乗の形になっているものは個別に積分することはできないので,被積分関数を展開してから原始関数を求めるのが基本. (II) 多項式の累乗の積分については次の公式がある. (x+a)ndx= +C (ax+b)ndx= +C (III) 2次関数のグラフと直線とで囲まれた図形の面積を求めるときに,次の公式を用いると便利である. ax2+bx+c=0 の2つの解を α,β (α<β) とするとき (ax2+bx+c)dx=− あるいは a(x−α)(x−β)dx=− (III)は,(II)の結果を用いて次のように証明できる. (ax2+bx+c)dx=a(x−α)(x−β)dx =a(x−α)(x−α+α−β)dx =a{(x−α)2+(α−β)(x−α)dx = a+a(α−β) =a+a(α−β)−0=a−a =− |
(I)の例 (x−1)(x−2)dx=(x2−3x+2)dx=−x2+2x =( 9−+6)−0= (x+1)2dx=(x2+2x+1)dx=+x2+x =( +4+2)−( +1+1)= (II)の例 (x+1)2dx=+C (2x+1)4dx=+C (III)は次のア)のように積分区間の両端が ax2+bx+c=0 の2つの解 α,β になっているときだけ成立し,イ)のように積分区間の両端が ax2+bx+c=0 の解でないときは(III)の公式は使えないので注意を要す.  2x2−6x+1=0 の2つの解を α,β とすると,α,β= β−α= このとき,(2x2−6x+1)dx=−=−=− ※積分区間の両端が根号を含む式で表わされるときは,この公式があると助かる. |
| 問題3 次の定積分を求めよ.(空欄を埋めよ) |
(1) (積の形で書かれた多項式は,展開してから積分を求めるのが基本) (x−1)(x+2)dx =(x2+x−2)dx=+−2x =( +2−4)−(0) = (2) (2x−3)2dx =(4x2−12x+9)dx =−6x2+9x=( −24+18)−( −6+9) = (この問題は (II) の公式でも解くことができる) (3) x2(x2−1)dx =(x4−x2)dx =−=( −)−(−+) = (4) (x−1)(x−2)dx =(x2−3x+2)dx =−+2x=( −6+4)−( −+2) =− (この問題は (III) の公式を用いて,α=1 , β=2 , β−α=1 とすれば直ちに解ける.) (5) 2x2−8x+5=0 の2つの解を α,β (α<β) とするとき α= , β= , β−α= だから (2x2−8x+5)dx =−=− =−2 |
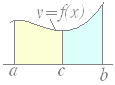
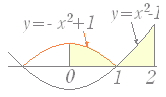
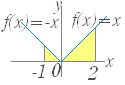
 [なぜ0で分けるのか]
[なぜ0で分けるのか]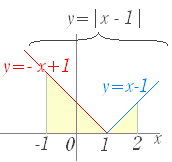 [積分区間をどのように分けるのか]
[積分区間をどのように分けるのか]