|
現在地と前後の項目 不定積分(解説)/不定積分1/不定積分２/不定積分(展開)/不定積分,変数t,r,y/不定積分,積分定数の決定/定積分1/定積分2/定積分の計算/定積分で定義される関数/面積/絶対値付関数の積分/絶対値付関数の積分(2)/曲線で囲まれた図形の面積(1)/曲線で囲まれた図形の面積(2)/曲線で囲まれた図形の面積(3)/立体の体積/
I【ｎ次式の積分の公式】
∫xndx=  xn+1n+1+C (n≧0)…(1)【記号】 ddxF(x)=f(x) ⇔ ∫f(x)dx=F(x)+C
|
例１ddxx3=3x2 ⇔ ∫x2dx=x33+C 例２ ddxx4=4x3 ⇔ ∫x3dx=x44+C例３ ただし書きの部分 ddxx=1 ⇔ ∫1dx=∫dx=x+C∫1dx を ∫dxと略す。 ∫dxは∫1dxの略で、∫0dxの略ではない。 だから、∫dx=x+Cになる。 |
|
【解説】 微分の公式を思い出すと、 (x3)’=3x2または ddxx3=3x2(x3+1)’=3x2または ddx(x3+1)=3x2(x3+2)’=3x2または ddx(x3+2)=3x2のように、x3+C (Cは任意の定数)の形の関数を微分すると、いずれも3x2になる。（定数Cを微分すると0になるから） ○ ［用語］ このように「微分すると3x2になる」ような元の関数を関数3x2の原始関数または不定積分*といい ∫3x2dx で表す。 この問題では、 ∫3x2dx=x3+C が成り立つ。 不定積分（または原始関数）を求めることを積分するという。 ○ 一般に ddxF(x)=f(x)のとき ∫f(x)dx=F(x)+C と書く。 全く初めて見る記号で違和感があるときは、 ∫2xdx=x2+C とは（2xを積分するとx2+Cになるとは）、 ddxx2=2xのこと（x2+Cを微分すると2xになる）だと言い換えるとよい。 【公式の証明】 微分の公式 ddxxn=nxn−1ddx(xn+1)=(n+1)xnddx(xn+1n+1)=xnしたがって
∫xndx=
xn+1n+1+C |
○ ある関数を「親」に例え、その導関数（微分）を「子供」に例えるとき、「親が決まれば子供は決まる」が「子供を決めても親は決まらない」。 例えば、微分して3x2になる元の関数はx3だけとは限らず、x3+1 , x3+2 , x3+3 , …のように定数項だけ異なる関数もすべて微分すると3x2になる。 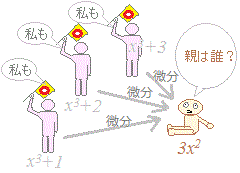 * F(x)の微分がf(x)になるときF(x)をf(x)の原始関数という。微分を指定しても原始関数はただ１通りには決まらず、定数項の分だけ不定になる。そこで、定数項Cの部分を不定にしたままで原始関数の集まりをF(x)+Cと表したものを不定積分という。 ○ 微分することを表す記号： ddxは、分母と分子を含めた全体で１つの記号となっており、一部分だけ約分したりすることはできない。 1xとはできない。○ よく似た約束が積分記号にもあり、積分記号は ∫f(x)dx のように前後をサンドイッチのようにはさんだ形で使い、片方だけではダメ。 読むときは「インテグラル・エフエックス・ディーエックス」などと読む。 ○ ∫の記号はアルファベットのSを縦長に引き延ばしたもの。 ○ ∫f(x)dxにおいてf(x)のことを被積分関数という。（積分される関数という意味） |
|
II【定数倍、和・差の積分の変形公式】
∫k f(x)dx=k∫f(x)dx …(1) ∫{f(x)+g(x)}dx=∫f(x)dx+∫g(x)dx …(2) ∫{f(x)−g(x)}dx=∫f(x)dx−∫g(x)dx …(3) ※ 積分定数Cはまとめて１つ付けるとよい。 (1)の例 ∫5x2dx=5∫x2dx=5 · x33+C= 53x3+Cのように定数k倍（この問題では5倍）は「後から」掛けてよい。 ※ 5∫x2dx=5( x33+C’)= 53x3+5C’だと思う人がいるかもしれないが、C’が実数全体のとき5C’が表すことのできる数は実数全体なので、改めて5C’=CとおけばCだけで書ける。5Cなどと書くとズッコケ答案になるので注意しよう。※ 「掛け算は何でも分けられる」訳ではなく、定数倍だけは後から掛けてよいという公式(1)の意味は間違いやすいので注意 例えば ∫x5dx= x66+Cは正しいが、∫x2·x3dx= x33 · x44+C= x712+Cは正しくない。このように「２つの関数の積」を積分するときに、各々の積分を求めて「後で掛けてもダメ」である。「後から掛ける」のが許されるのは「定数倍」（xのないもの）だけである。 だから ∫(x+1)(x+2)dx のように多項式の積になっているものを積分するときも、 ∫(x+1)dx∫(x+2)dx=( x22+x)( x22+2x)+Cなどとしてはいけない。 多項式の積分は「展開してから」公式(2)を利用して行う ∫(x+1)(x+2)dx=∫(x2+3x+2)dx = 13x3+32x2+2x+C |
(2)の例 ∫(x2+x)dx=∫x2dx+∫xdx= x33+x22+C※ ∫x2dx+∫xdx=( x33+C)+(x22+C)= x33+x22+2Cだと思う人がいるかもしれないが、それは違う。 ２つの不定積分 x33+Cとx22+Cの任意定数Cが等しいとは限らないので、この式を丁寧に書けば x33+C1+x22+C2 (C1 , C2は任意定数)になる。ところが、C1 , C2が任意定数のとき、C1+C2が表せる数は任意の実数なので、これらをまとめて単にCと書けばよい。 (3)は(2)と同様に考えるとよい。 ○ (1)(2)(3)を通して、任意定数C（不定積分で登場する任意定数は、積分定数と呼ばれる）の付け方のまとめ： ⇒ 「全体をまとめて１つの積分定数Cを後ろに１つ付けるとよい。」 ○ 被積分関数が積や商で結ばれているとき（ ）は必要ないが、和・差・負の符号を伴うときは被積分関数を（ ）で囲む必要がある。 ∫とf(x)とdxは、「積」として結ばれていると考えるとよい。 ∫●f(x)●dx
|
|
例 I(1) → ∫x4dx= x55+C∫xdx= x22+C∫dx=x+C II(1) → ∫3xdx= 3∫xdx=3 x22+C= 3x22+C∫5dx=5∫dx+C=5x+C |
II(2)(3) → 多項式の積分は「展開してから」公式(2)を利用して行う ∫(x−3)2dx= ∫(x2−6x+9)dx = x33−3x2+9x+C∫x(x+2)dx= ∫(x2+2x)dx = x33+x2+C■読み終わったら→ ここ ←をクリック■ |