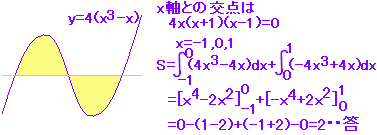|
■面積 解説 |
||
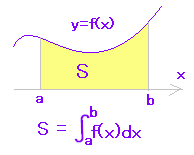
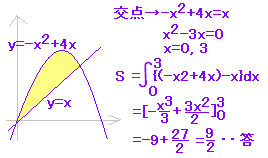
| (ア) y=f(x)のグラフがx軸よりも上にあるとき (f(x)≧0のとき)定積分は面積を表わします。
|
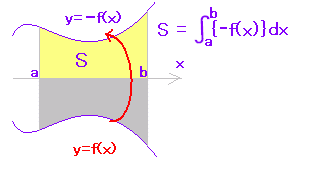
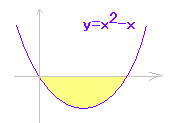
(イ) y=f(x)のグラフがx軸よりも下にあるとき (f(x)≦0のとき)y=-f(x)のグラフを作ると,このグラフはx軸よりも上にあるので,符号を変えた定積分は面積を表わします。
|
|
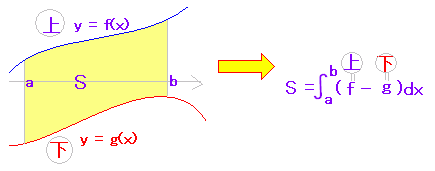
(ウ) f(x)≧g(x)≧0のとき,次のように2つの面積の差が2曲線の間にある図形の面積になります。(切り紙のイメージで考えます。)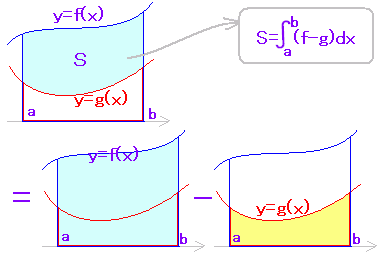 |
(エ) f(x)≧g(x)であれば,形・面積が変わらないように持ち上げるとg(x)≧0となり2つの面積の差が2曲線の間にある図形の面積になります。→(ウ)になります。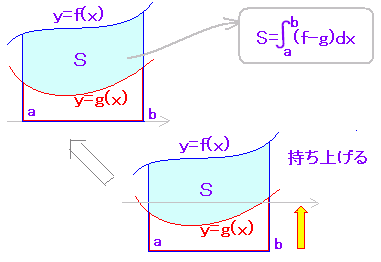 |
|
| ◆◆まとめ◆◆・・・以上の(ア)〜(エ)は(エ)でまとめることができます。 | ||
| ○ 面積は ∫{ (上) - (下) }dx ・・・ x軸より下にあってもこれでよい。
|
||
| 「キュウリもみ」を作ったことがありますか? 「(上)-(下)という長さ」のキュウリの断片を x軸上に集めているのと同じことです。 |
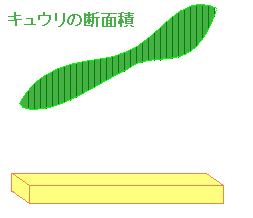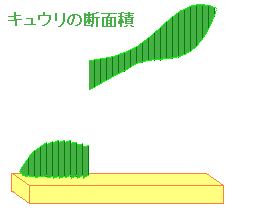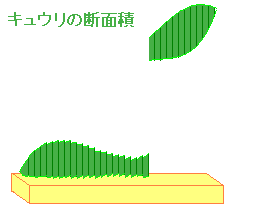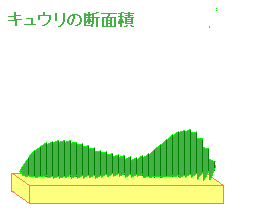 |
|
初めの公式の見直し:(ア) 上がy=f(x),下がy=0と見ます。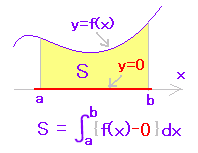 |
初めの公式の見直し:(イ) 上がy=0,下がy=f(x)と見ます。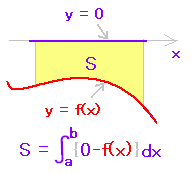 |
|