|
亂
n偑惓偺惍悢乮1, 2, 3, …乯偺偲偒 偨偩偟 堦斒偵掕悢崁偺愊暘偼
乮拲乯
 |
(1)偺晄掕愊暘傪棙梡偡傞掕愊暘偺寁嶼偺椺 (2)偺晄掕愊暘傪棙梡偡傞掕愊暘偺寁嶼偺椺 (3)偺晄掕愊暘傪棙梡偡傞掕愊暘偺寁嶼偺椺 |
|
亂
n偑惓偺惍悢乮1, 2, 3, …乯偺偲偒 偨偩偟 堦斒偵掕悢崁偺愊暘偼
乮拲乯
 |
(1)偺晄掕愊暘傪棙梡偡傞掕愊暘偺寁嶼偺椺 (2)偺晄掕愊暘傪棙梡偡傞掕愊暘偺寁嶼偺椺 (3)偺晄掕愊暘傪棙梡偡傞掕愊暘偺寁嶼偺椺 |
|
亂栤戣侾亃丂師偺掕愊暘傪媮傔偰偔偩偝偄丏乮慖戰巿偺拞偐傜惓偟偄傕偺傪侾偮僋儕僢僋乯
(1)
|
(2)
|
|
(3)
|
(4)
|
|
亂愊暘曄悢偑x埲奜偺応崌亃 乑 仜晄掕愊暘偱偼娭悢偑巆傞偺偱丆寁嶼偺寢壥偼愊暘曄悢偵埶懚偟傑偡偑丆掕愊暘偱偼尨巒娭悢偵忋抂丒壓抂偺抣傪戙擖偡傞偺偱愊暘曄悢偼寁嶼寢壥偵巆傝傑偣傫丅 仜偙偺傛偆偵掕愊暘偱偼丆愊暘曄悢傪擖傟懼偊偰傕寢壥偼曄傢傜偢丆娭悢宍偲愊暘嬫娫偺忋抂丒壓抂偺抣偩偗偑廳梫偱偡丅 仜愊暘曄悢偑 |
亂晄掕愊暘亃
亂掕愊暘亃 |
|
亂栤戣俀亃丂師偺掕愊暘傪媮傔偰偔偩偝偄丏乮慖戰巿偺拞偐傜惓偟偄傕偺傪侾偮僋儕僢僋乯
(1)
|
(2)
|
|
(3)
|
(4)
|
|
亂旐愊暘娭悢偑愊偺宍偵側偭偰偄傞偲偒亃 仜 偄傞偲偒偼丆揥奐偟偰偐傜晄掕愊暘傪媮傔丆掕愊暘傪峴偄傑偡丏 仸暿乆偵愊暘偟偨傕偺傪屻偐傜妡偗偰傕丆惓偟偄寢壥偵側傝傑偣傫丏 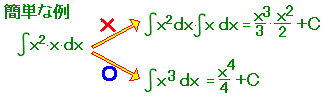
|
亂梫揰亃懡崁幃偼丆揥奐偟偰偐傜愊暘偡傞丏
佱椺1佲 佱椺2佲 佱嶲峫佲丂悢妛嘦偱偼丆乽懡崁幃偼揥奐偟偰偐傜愊暘偡傞乿偲偄偆偺偑婎杮偱偡偑丆敪揥妛廗偲偟偰師偺岞幃傑偱娷傔傞応崌偑偁傝傑偡丏乮晄掕愊暘偵娭偟偰乯 丂偙偺岞幃偼丆悢妛嘦+悢妛B偺斖埻偱偼丆悢妛揑婣擺朄偱徹柧偱偒傑偡偑丆悢妛嘨偱偼崌惉娭悢偺旝暘朄傕偟偔偼抲姺愊暘偺撪梕偲側偭偰偄傑偡丏 |
|
亂栤戣俁亃丂師偺掕愊暘傪媮傔偰偔偩偝偄丏乮慖戰巿偺拞偐傜惓偟偄傕偺傪侾偮僋儕僢僋乯
(1)
|
(2)
|
|
(3)
|
(4)
|
|
仭乵屄暿偺暸偐傜偺幙栤偵懳偡傞夞摎乶[掕愊暘丗婎杮寁嶼偵偮偄偰乛17.8.16乶
暘偐傝傗偡偄偱偡
拞恎偑壗忔偵側偭偰傞偲偒偺岞幃(愢柧壓庤偱偡傒傑偣傫)偲偐懠偺岞幃傕堦弿偵嫵偊偰傎偟偄偱偡媰
仭乵屄暿偺暸偐傜偺幙栤偵懳偡傞夞摎乶[掕愊暘丗婎杮寁嶼偵偮偄偰乛17.8.11乶
亖亜乵嶌幰乶丗楢棈偁傝偑偲偆丏幙栤偲夞摎偲偑惓妋偵懳墳偟偰偄傞偐偳偆偐暘偐傝傑偣傫偑丆偙偺嫵嵽偼悢妛嘦偺掕愊暘偺嫵嵽偱偡丏 嶲峫彂傗庼嬈偺拞偱偼丆妋偐偵侾師幃偺値忔偺愊暘傪埖偆応崌傕偁傞傛偆偱偡偑丆偦偺徹柧偵偼抲姺愊暘乮傑偨偼崌惉娭悢偺旝暘朄乯傪昁梫偲偟傑偡偺偱丆悢妛嘦偱嫵偊傞偺偼柍棟偑偁傞傛偆偱偡丏偟偨偑偭偰丆悢妛嘦偱埖偭偰偄傞応崌偼丆偨偩扨偵摢偛側偟偵乽妎偊偲偗両乿偲尵偭偰偄傞偩偗偱椙怱揑側嫵偊曽偵偼尒偊側偄偺偱巹偺応崌偼悢妛嘨偱嫵偊傞傛偆偵偟偰偄傑偡丏 曄悢暥帤偺庬椶偱偁傞掱搙憐掕偱偒傞偺偱丄栤戣偲偟偰偼摨偠暥帤傪巊偭偨曽偑椙偄姶偠偑偟偨丅
媣乆偵乮係侽擭傇傝偵乯掕愊暘傪愢偄偰傒偨丅堄奜偲柺敀偄丅
亖亜乵嶌幰乶丗楢棈偁傝偑偲偆丏偁傞掱搙暘偐偭偰偄傞恖偺姶憐偺傛偆偱偡偑丆偙偺彫崁栚偼乽嬫娫偺椉抂偑掕悢偱偁傞偲偒丆愊暘曄悢偲旐愊暘娭悢偑摨偠暥帤偱偁傟偽丆掕愊暘偺抣偼撪晹曄悢偺庬椶偵埶懚偟側偄乿偲偄偆偙偲傪妛傇偨傔偺嫵嵽側偺偱丆堎側傞曄悢偱楙廗偟側偄偲偦傕偦傕楙廗偵側傜側偄偺偱偡丏 乽偦傟傜偼傒側摨偠傕偺偩乿偲偄偆偙偲偑暘偐偭偰偄傞偲丆壗傪僋僪僋僪偲摨偠榖傪孞傝曉偟偰偄傞偺偐偲偄偆傛偆偵尒偊傑偡偑丆偁側偨偼偦偺僴乕僪儖傪愄偵柍帠偵捠夁偟偰偄傞偺偱丆壗偑僴乕僪儖側偺偐棅傝側偔姶偠傞偺偐傕偟傟傑偣傫丏 |