|
→ スマホ用は別頁
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
難易度の目安 基 本:★☆☆
普 通:★★☆
やや難:★★★
|
|
→ スマホ用は別頁
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
難易度の目安 基 本:★☆☆
普 通:★★☆
やや難:★★★
|
|
【Ⅰ.1.(1) 楕円の方程式】
2定点F(c, 0), F’(−c, 0)からの距離の和が一定2aである点P(x, y)の軌跡は楕円になる. (ただし,a>c>0とし,
• a, b, cの図形的な対応は,動点Pがy軸上の点Bに重なるときを考えると,分かり易い.(下図)
• 直角三角形OFBについて,三平方の定理を考えるとよい. 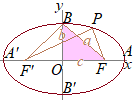 • 楕円の方程式は
• 楕円の方程式は• 焦点の座標は • 長軸の長さは,AA’=2a (一般に,a>b>0のとき,AA’が長軸になる.右図はこれに該当する.) • 短軸の長さは,BB’=2b (一般に,a>b>0のとき,BB’が短軸になる.右図はこれに該当する.) • 一定となる距離の和は,FP+PF’=2a |
【Ⅰ.1.(2) 楕円の方程式】
証明は(1)のときと同様に行えばよい
2定点F(0, c), F’(0, −c)からの距離の和が一定2bである点P(x, y)の軌跡は楕円になる. (ただし,b>c>0とし, 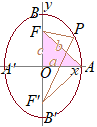 • 楕円の方程式は
• 楕円の方程式は• 焦点の座標は • 長軸の長さは,BB’=2b (一般に,b>a>0のとき,BB’が長軸になる.右図はこれに該当する.) • 短軸の長さは,AA’=2a (一般に,b>a>0のとき,AA’が短軸になる.右図はこれに該当する.) • 一定となる距離の和は,FP+PF’=2b |
|
[楕円の方程式(1)の証明] 動点をP(x, y)とおいて,2点F(c, 0), F’(−c, 0)との距離の和を求めると
このまま両辺を2乗しても「一応計算できる」が「途中経過が4次式のコテコテの計算になる」から,そっちに進むのは避ける方がよい.
次のように根号を両辺に分けてから2乗すると,少しは簡単になる. 辺々2乗する 辺々2乗する ここで,
以上の証明の途中経過を覚える必要はない.後の参考としては「根号を両辺に分けてから2乗する」という変形の勘を身に着けておく程度とする.
|
【例題1】★☆☆
a=3, b=2 (a>b>0)だから楕円 (高校教科書のレベル)
(1) 焦点の座標は, (2) 長軸の長さは,(2a=)6
♣♦--危険なワナ--♥♠
(3) 短軸の長さは,(2b=)4→ (a=)3は長軸の長さではない.aは,ほぼ≃半径
♣♦--危険なワナ--♥♠
→ 上記と同様. 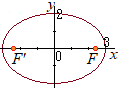 (4) グラフの概形は右図
(4) グラフの概形は右図(「がいけい」とは,だいたいの形のこと.手書きだから,完全に正確なグラフは無理.大体の形で,要点を押さえていればよい)
【例題2】★☆☆
楕円 (高校教科書のレベル)
と変形する. 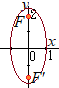 a=1, b=2 (b>a>0)だから
a=1, b=2 (b>a>0)だから(1) 焦点の座標は, (2) 長軸の長さは,(2b=)4 (3) 短軸の長さは,(2a=)2 (4) グラフの概形は右図 |
|
【例題3】★☆☆
(1)次の楕円について,(A) 焦点の座標, (B) 長軸の長さ, (C) 短軸の長さを求めて,(D) グラフの概形を描いてください. (1) (2) (高校教科書のレベル)
(A) 焦点の座標は 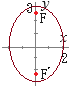 (B) 長軸の長さは
(B) 長軸の長さは(C) 短軸の長さは (D) 概形は,右図の通り と変形できる (A) 焦点の座標は 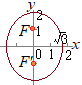 (B) 長軸の長さは
(B) 長軸の長さは(C) 短軸の長さは (D) 概形は,右図の通り |
【問題1】★☆☆
[解説を読む]xy平面上の2点F(1, 0), F’(−1, 0)からの距離の和がつねに4であるような点の軌跡はだ円となる.このだ円の長軸と短軸の長さを求めよ. (2000年度北海道工大)
動点の座標をP(x, y)とおくと,PF+PF’=4より
このままで両辺を2乗しても「一応計算できる」が「途中経過が4次式のコテコテの計算になる」から,そっちに進むのは避ける方がよい.
次の変形のように根号を両辺に分けてから2乗すると,少しは簡単になる. 辺々を2乗する 辺々を2乗する 長軸の長さは (別解)・・・結果がだ円になることは,問題文に書かれているから,だ円の公式に当てはめると 長軸の長さは  |
|
【Ⅰ.2.(1)双曲線の方程式】
2定点F(c, 0), F’(−c, 0)からの距離の差が一定±2aである点P(x, y)の軌跡は双曲線になる. (ただし,c>a>0とし, 双曲線 • 焦点の座標は 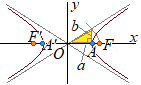 • 主軸はx軸(右図の通り)
• 主軸はx軸(右図の通り)• 漸近線の方程式は • 頂点の座標は A(a, 0), A’(−a, 0) • 双曲線の中心は原点O(0, 0) |
【Ⅰ.2.(2) 双曲線の方程式】
2定点F(0, c), F’(0, −c)からの距離の差が一定±2bである点P(x, y)の軌跡は双曲線になる. (ただし,c>b>0とし, 双曲線 • 焦点の座標は 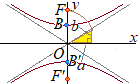 • 主軸はy軸(右図の通り)
• 主軸はy軸(右図の通り)• 漸近線の方程式は • 頂点の座標は B(0, b), B’(0, −b) • 双曲線の中心は原点O(0, 0) |
|
[双曲線の方程式(1)の証明] 動点をP(x, y)とおいて,2点F(c, 0), F’(−c, 0)との距離の差を求める.(ただし,c>a>0)
このまま両辺を2乗しても「一応計算できる」が「途中経過が4次式のコテコテの計算になる」から,そっちに進むのは避ける方がよい.
次のように根号を両辺に分けてから2乗すると,少しは簡単になる. 辺々2乗する 辺々2乗する
ここで,c>a>0に注意する
ここで, |
【例題4】★☆☆
(1)次の双曲線について,(A) 焦点の座標, (B) 頂点の座標, (C) 漸近線の方程式を求めて,(D) グラフの概形を描いてください. (1) (2) (高校教科書のレベル)
(A) 焦点の座標は (B) 頂点の座標は (C) 漸近線の方程式は 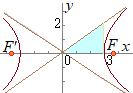 (D) 概形は,右図の通り
(D) 概形は,右図の通り(A) 焦点の座標は 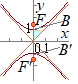 (B) 頂点の座標は
(B) 頂点の座標は(C) 漸近線の方程式は (D) 概形は,右図の通り |
|
【例題5】★☆☆
a=4, b=3だから双曲線 (高校教科書のレベル)
(1) 焦点の座標は, (2) 頂点の座標は,A(4, 0), A’(−4, 0)) 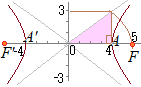 (3) 漸近線の方程式は,
(3) 漸近線の方程式は,(3) グラフの概形は右図 |
【問題2】★☆☆
[解説を読む]双曲線 (2011年度日本大 理工学部)
|
|
【問題3】★★★
[解説を読む]2定点F(a, a), F’(−a, −a)を焦点とし,F, F’からの距離の差が2aである双曲線Cを考える.ただし,a>0とする. (1) 双曲線Cの方程式を求めよ. (2) 双曲線Cの頂点の座標および漸近線の方程式を求めよ. (2000年度鹿児島大)
(1)
動点をP(x, y)とおく 辺々2乗する 辺々2乗する (2) (1)の形の直角双曲線の漸近線は,座標軸である 頂点の座標は,y=±xの直線と双曲線との交点として求まる. |
(別解)・・・問題文にも結果が双曲線になると書かれているので,これを利用した答案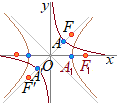 x軸上の
x軸上の双曲線の方程式は 漸近線の方程式は 上記の焦点,頂点,漸近線,双曲線を原点の周りに45°反時計回りに回転させる.次の変換により新座標(X, Y)が求まる.
•焦点の座標は
•頂点の座標は ・・・(2)の答 •漸近線の方程式は •双曲線の方程式は 変数をx, yで書くと |
|
【Ⅰ.3.(1) 放物線の方程式】
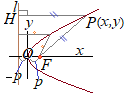 • 焦点F(p, 0)と準線x=−p (p≠0)からの距離が等しい点
• 焦点F(p, 0)と準線x=−p (p≠0)からの距離が等しい点P(x, y)の軌跡は放物線 • p≠0のとき,放物線
(1) 頂点は,原点O(0, 0)
放物線の対称軸のことを,単に軸という.(2) 焦点の座標は,F(p, 0) (3) 準線の方程式は,x=−p
(4) 軸の方程式は,y=0
|
【Ⅰ.3.(2) 放物線の方程式】
この方程式は,.においてxとyの役割を入れ替えたものとなっている.
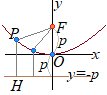 • 焦点F(0, p)と準線y=−p (p≠0)からの距離が等しい点
• 焦点F(0, p)と準線y=−p (p≠0)からの距離が等しい点P(x, y)の軌跡は放物線 • p≠0のとき,放物線
(1) 頂点は,原点O(0, 0)
(2) 焦点の座標は,F(0, p) (3) 準線の方程式は,y=−p (4) 軸の方程式は,x=0 |
(放物線の方程式 .の証明)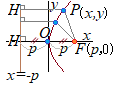
初めに,準線上の点Hと動点P(x, y)および焦点F(p, 0)が一直線上に並ぶとき,HP=PFとなる.すなわち,動点P(x, y)は原点O(0, 0)を通ることに注意.
動点の座標をP(x, y),動点から準線x=−pに下ろした垂線の足を(−p, y),焦点の座標をF(p, 0)とおくとこのように定めると放物線の頂点が原点を通ることになり,方程式が簡単になる. 応用問題としては,頂点が原点以外に来る場合も扱うが,準線の方程式x=−pと焦点の座標F(p, 0)とで,符号だけ異なる数値p, −pを使うのは,このように頂点を原点に一致させるねらいがあるからと考えればよい. 辺々2乗する |
【例題6】★☆☆
(1)次の放物線について,(A) 焦点の座標, (B) 頂点の座標, (C) 準線の方程式を求めて,(D) グラフの概形を描いてください. (1) (2) (高校教科書のレベル)
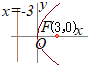 (A) 焦点の座標は
(A) 焦点の座標は(B) 頂点の座標は (3) 準線の方程式は (D) 概形は右図の通り 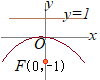 (A) 焦点の座標は
(A) 焦点の座標は(B) 頂点の座標は (3) 準線の方程式は (D) 概形は右図の通り |
|
【Ⅱ. 曲線の平行移動】
一般に,曲線 f(x, y)=0をx軸の正の向きにp,y軸の正の向きにqだけ平行移動して得られる曲線の方程式は f(x−p, y−q)=0 x軸の正の向きにα,y軸の正の向きにβだけ平行移動するとき (1) 楕円 (2) 双曲線 (3) 放物線 |
【例題7】★☆☆
(1)(1) 楕円 (2) (高校教科書のレベル)
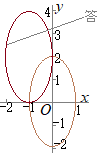 (2)
(2)は楕円 |
|
【問題4】★★☆
[解説を読む]座標平面上の点(x, y)が曲線 (2016年度産業医科大)
ただし より,0≦x≦6, −2≦y≦2・・・② ①を ②により,x=3, y=±2のとき最小値−5をとる・・・(答) (別解1) ただし より,0≦x≦6, −2≦y≦2・・・④ を用いて,xを消去し,1変数yの関数に直してもよい ④により,x=3, y=±2のとき最小値−5・・・(答) (別解2) 媒介変数を用いて1つの変数で表す方法 より,x=3cosθ+3, y=2sinθ (0≦θ<2π)・・・⑤ とおけるから 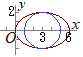 (別解3)
(別解3)点Pが右図の茶色で示した曲線 x=3, y=±2のとき最小値−5・・・(答) |
【例題8】★☆☆
(1)(1) 双曲線 (2) (高校教科書のレベル)
(2) 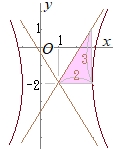
双曲線
【問題5】★★☆
[解説を読む]方程式 (2011年度慶應義塾大 医学部)
と変形できるから,(2)は双曲線 を,x軸の正の向きに−2,y軸の正の向きに1だけ平行移動したもの
【例題9】★☆☆
(1)(1) 放物線 (2) (高校教科書のレベル)
(2) 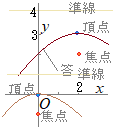 放物線
放物線 |
 ■因数分解型の不等式が表す図形■
■因数分解型の不等式が表す図形■2文字の因数分解型の不等式が表す図形は,市松模様(チェック模様)とも呼ばれ,東京2020のエンブレムや『鬼滅の刃』炭治郎の上着にも用いられている.歌舞伎役者 佐野川市松が好んで用い,後に市松模様などと呼ばれるようになった. • 市松模様では,境界線で隣り合う領域は白黒が反対になり,対角線側とは一致する. • 因数分解型の不等式は,連立不等式の応用問題と考えることができ,例えば, という因数分解型の不等式は 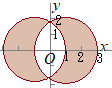
または 右図の茶色で塗った箇所に対応する. • このような市松模様を作るには, のような形では,できない. • 「市松に塗り分ける」「柄模様が市松になっている」などと形容動詞的に使うこともあるようです. |
【問題6】★★☆
[解説を読む]次の不等式が表す領域を座標平面上に図示しなさい. (2016年度龍谷大 理工学部)
①②の交点は 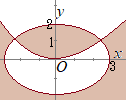 例えば,点x=1, y=0は原式を満たさないので,点(1, 0)を含む領域は塗りつぶさない.その隣の領域から塗り始めて,市松に塗りこむ.ただし,境界線は含まない.
例えば,点x=1, y=0は原式を満たさないので,点(1, 0)を含む領域は塗りつぶさない.その隣の領域から塗り始めて,市松に塗りこむ.ただし,境界線は含まない.(点x=0, y=1は原式を満たすので,点(0, 1)を含む領域を塗りつぶし,順に市松に塗りつぶす.ただし,境界線は含まない.) 右図の塗りこんだ部分が解 |
|
【基本の復習】
•不等式 •不等式 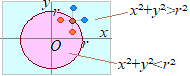 •不等式 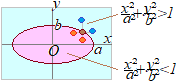 |
【問題7】★★☆
[解説を読む]xy平面において,不等式 が表す領域の面積を求めよ. (2014年度横浜国立大 理工学部)
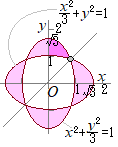 右図の桃色で示した部分.濃い桃色の部分の面積を求めて8倍すればよい.
右図の桃色で示した部分.濃い桃色の部分の面積を求めて8倍すればよい.灰色で示した交点のx座標は から求まる 濃い桃色の部分の面積は 定積分の所は,各々置換積分によって計算できる
濃い桃色の部分の面積は 求める面積は |
|
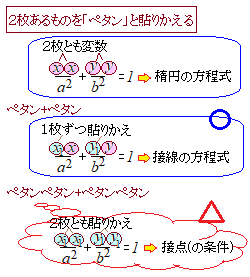
【Ⅲ.1 接線の公式】
• 放物線の方程式で,「変数+変数」と読める所は「1枚を接点の座標に入れ換えた足し算」にすると接線の方程式になる.
※ 勢い余って,「1つの変数を2枚とも」貼りかえてしまうと,接点が曲線上にあるという事実を表すだけになるので要注意.
|
(接線の公式:証明) 楕円,双曲線,放物線上の接点 (A) 内容的には,数学Ⅲの「陰関数の微分法」を用いると統一的に示せる. (A) 楕円 ①の両辺を陰関数の微分法によって微分する したがって,接点 (なお, 接線の方程式は |
|
双曲線 ②の両辺を陰関数の微分法によって微分する したがって,接点 (なお, 接線の方程式は 双曲線 |
放物線 ③の両辺を陰関数の微分法によって微分する したがって,接点 (なお, 接線の方程式は |
|
【例題10】★☆☆
(1)(1) 楕円 (2) 双曲線 (3) 放物線 (高校教科書のレベル)
(2) (3) |
【問題8】★☆☆
[解説を読む]楕円 (2011年度長崎大 工学部)
【問題9】★☆☆
[解説を読む]楕円 (ア) 0 (カ) 1 (サ) 2 (タ) 3 (ナ) 4 (ハ) 5 (マ) 6 (ヤ) 7 (ラ) 8 (ワ) 9 (2014年度自治医科大)
|
|
【Ⅲ.2 接線の公式】
|
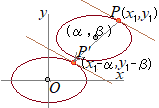 (証明)
(証明)• 楕円 上の接点を と,楕円上の接点 このグラフを,x軸の正の向きにα,y軸の正の向きにβだけ平行移動すると,接点 • 双曲線,放物線の場合も,同様にして示せる. |
|
【例題11】★☆☆
(1)(1) 楕円 (2) 双曲線 (3) 放物線 (高校教科書のレベル)
(2) (3) |
【極線の方程式Ⅳ】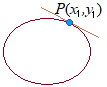
(1) 点 は,点 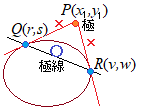 を表さず,点
を表さず,点
• 公式:
• 次に,点 |
|
(2) 点
(証明)
点Pを通る2つの接線の接点QとRを結ぶ直線QRになる. このとき,直線QRは,点Pを極とする極線と呼ばれる. 2つの接点をQ(r, s), R(v, w)とおくと,接線の方程式は,各々 これら2つの接線は,点 ここで,(なぜ思いつくのかは別として) という(直線の)方程式を考えてみると,①’,②’は,③にQ(r, s), R(v, w)の座標を代入したら,成り立つということを表している. したがって,③はQ(r, s), R(v, w)を結ぶ直線になる・・・■証明終■
【例題12】★★☆
(1) 楕円 (2) 楕円 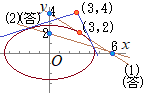 (1)
(1)
(2)
※一般に,x切片がa,y切片がb(ただし,a, b≠0)である直線の方程式は
|
(3) 点
(証明)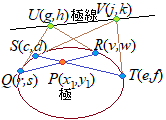
点Pを通る直線と曲線との交点Q, Rを接点とする2つの接線の交点をUとする. 同様にして,点Pを通る別の直線と曲線との交点S, Tを接点とする2つの接線の交点をVとする.(異なる2つ以上の直線であれば,何本引いてもよいが,最小限2本引けばよい) ①は,これら2つの点U, Vを結ぶ直線UVになる. このとき,直線①は,点Pを極とする極線と呼ばれる. 前述の(2)と同様に考えるが,途中経過はかなり長くなる. Q(r, s), R(v, w)を接点とする2つの接線の交点がU(g, h)だから U(g, h)は②も③も満たすから ②’, ③’は,直線 上に2点Q(r, s), R(v, w)があることを示している. S(c, d), T(e, f)を接点とする2つの接線の交点がV(j, k)だから,同様にして,次の関係式が成り立つ ⑤⑥は,2点U(g, h), V(j, k)が直線 上にあることを示している.・・・■証明終■ |