|
ЃЎ‹ЙЌА•W
Ѓy‹ЙЌА•W‚Ж‚НЃz
Ѓ¦‹ЙЌА•W‚Ж‚µ‚Д‚Н’КЏнrЃ†0‚М‚а‚М‚р€µ‚ў‚Ь‚·‚ЄЃC•K—v‚Й‰ћ‚¶‚Дr<0‚Ж‚И‚й•\Њ»‚аЋg‚н‚к‚й‚±‚Ж‚Є‚ ‚и‚Ь‚·ЃDr<0‚М‚Ж‚«‚НЃC”јЊa‚Єђі‚Е•ОЉp‚ЄѓЖ+ѓО‚М“_‚р•\‚·‚а‚М‚Ж‚µ‚Ь‚·ЃDЃ@•Ѕ–КЏг‚М“_‚рЃCЊґ“_‚©‚з‚М‹——Јr‚ЖЋnђьЃixЋІ‚Мђі‚МЊь‚«Ѓj‚©‚з‚М•ОЉpѓЖ‚М‘g(r, ѓЖ)‚Е•\‚µ‚Ѕ‚а‚М‚р‹ЙЌА•W‚Ж‚ў‚ў‚Ь‚·ЃD 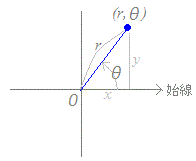 Ѓ¦’†ЉwЌZ‚ЕЏK‚Б‚Ѕ’јЊрЌА•W(x,y)‚Ж‹ЙЌА•W(r, ѓЖ)Ѓi‚Ѕ‚ѕ‚µЃCrЃ†0‚Ж‚·‚йЃDЃj‚Ж‚НЃCЋџ‚МЉЦЊW‚Є‚ ‚и‚Ь‚·ЃD Ѓm‹ЙЌА•WЃЁ’јЊрЌА•WЃn
x=r cosѓЖ
Ѓm’јЊрЌА•WЃЁ‹ЙЌА•WЃn
y=r sinѓЖ
r=
ѓЖ‚Н
cosѓЖ=
‚Ж‚И‚йЉp
sinѓЖ= |
 Ѓy—бЃz
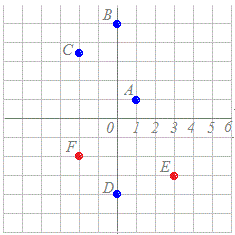
Ѓy—бЃz(1) ‰Eђ}‚МA ’јЊрЌА•W‚Н(1,1) ‹ЙЌА•W‚Н(,) (2) ‰Eђ}‚МB ’јЊрЌА•W‚Н(0,5) ‹ЙЌА•W‚Н(5,) (3) ‰Eђ}‚МC ’јЊрЌА•W‚Н(−2,2) ‹ЙЌА•W‚Н(4,) (4) ‰Eђ}‚МD ’јЊрЌА•W‚Н(0,−4) ‹ЙЌА•W‚Н(4,) (*) ђ}‚М“_E ‹ЙЌА•W‚Ж‚µ‚Д(3,−)‚̂悤‚ЙѓЖ<0‚Ж‚И‚йЉp“x‚рЋg‚¤‚±‚Ж‚Є‚ ‚и‚Ь‚·ЃD Ѓ@€к”К‚ЙЃCѓЖ+2nѓОЃin‚Нђ®ђ”Ѓj‚Н‚·‚Ч‚Д“Ї‚¶•ОЉp‚р•\‚·ЃD‹ЙЌА•W(r, ѓЖ)ЃЁђ}‚М‘О‰ћ‚Н‚Ѕ‚ѕ‚P’К‚и‚Е‚ ‚й‚ЄЃCђ}ЃЁ(r, ѓЖ)‚МЏкЌ‡‚НЃC—Ⴆ‚О•ОЉp‚р0Ѓ…ѓЖ<2ѓО‚М”Н€Н‚Е’и‚Я‚й‚±‚Ж‚Й‚·‚к‚ОЃCѓЖ‚Н‚Ѕ‚ѕ‚P’К‚и‚Й’и‚Ь‚и‚Ь‚·ЃD (*) ђ}‚М“_F ‹ЙЌА•W‚Ж‚µ‚Д(−2,)‚̂悤‚Йr<0‚Ж‚И‚йЏкЌ‡‚Н (2,)‚Ж“Ї‚¶‚Й‚И‚и‚Ь‚·ЃD |
|
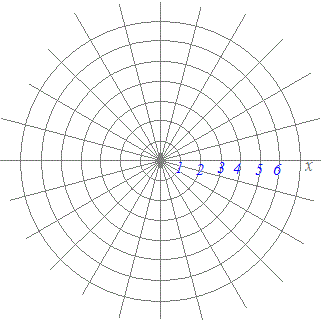
Ѓy–в‘и‚PЃz‹ЙЌА•W(r, ѓЖ)‚Е•\‚і‚к‚ЅЋџ‚М“_‚М€К’u‚р‰Eђ}‚М’†‚ЕѓNѓЉѓbѓN‚µ‚Д‚‚ѕ‚і‚ўЃDЃi‚ ‚И‚Ѕ‚М“љ€Д‚Н
‚W–в‚ ‚и‚Ь‚·ЃЁ[‘ж1–в / ‘S8–в] ‰рђа NEXT
Ѓy–в‘и‚QЃzЋџ‚М‹ЙЌА•W(r, ѓЖ)‚р’јЊрЌА•W(x, y)‚Й’ј‚µ‚Д‚‚ѕ‚і‚ўЃD
Ѓiђі‚µ‚ў‚а‚М‚р‘I‚с‚Е‚‚ѕ‚і‚ўЃDЃj
(1)(2, )
‰рђа(−,1) (−1, ) (−, ) (−, ) x=2×cos=2×(−)=−1 y=2×sin=2×()= ‚ѕ‚©‚зЃC(−1, ) (2)(2, ) ‰рђа (2, 2) (2, −2) (−2, 2) (−2, −2) x=2×cos=2×(−)=−2 y=2×sin=2×=2 ‚ѕ‚©‚зЃC(−2, 2) (3)(6, −) ‰рђа (3, −3) (−3, −3) (2, −2) (−2, 2) x=6×cos(−)=6×=3 y=6×sin(−)=6×(−)=−3 ‚ѕ‚©‚зЃC(3, −3) ‘±‚ЃЁ
|
(4)(5, ѓЖ)Ѓ@‚Ѕ‚ѕ‚µЃCѓЖ‚НЃCsinѓЖ=−, cosѓЖ=‚Ж‚И‚йЉp ‰рђа (, −) (−, ) (3, −4) (−4, 3) x=5×cosѓЖ=5×=3 y=5×sinѓЖ=5×(−)=−4 ‚ѕ‚©‚зЃC(3, −4) |
|
Ѓy–в‘и‚RЃzЋџ‚М’јЊрЌА•W(x, y)‚р‹ЙЌА•W(r, ѓЖ)‚Й’ј‚µ‚Д‚‚ѕ‚і‚ўЃD‚Ѕ‚ѕ‚µЃCrЃ†0, 0Ѓ…ѓЖ<2ѓО‚Ж‚µ‚Ь‚·ЃD
Ѓiђі‚µ‚ў‚а‚М‚р‘I‚с‚Е‚‚ѕ‚і‚ўЃDЃj
(1)(0, −5)
‰рђа(5, 0) (5, ) (5, ѓО) (5, ) ђ}‚рЌl‚¦‚к‚О–ѕ‚з‚©‚Ȃ悤‚ЙЃCѓЖ= ‚µ‚Ѕ‚Є‚Б‚ДЃC(5, ) (2)(, 1) ‰рђа (2, ) (2, ) (4, ) (4, ) r===2 cosѓЖ= , sinѓЖ=(0Ѓ…ѓЖ<2ѓО) ‚ж‚иѓЖ= ‚µ‚Ѕ‚Є‚Б‚ДЃC(2 , ) |
(3)(−3 , 3)
‰рђа (3, ) (3, ) (3, ) (3, ) r===3 cosѓЖ==− , sinѓЖ==(0Ѓ…ѓЖ<2ѓО) ‚ж‚иѓЖ= ‚µ‚Ѕ‚Є‚Б‚ДЃC(3 , ) (4)(2 , −2) ‰рђа (2, ) (2, ) (4, ) (4, ) r===4 cosѓЖ== , sinѓЖ=−=−(0Ѓ…ѓЖ<2ѓО) ‚ж‚иѓЖ= ‚µ‚Ѕ‚Є‚Б‚ДЃC(4 , ) |