|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
|
|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
|
|
(1) �ȉ~
�̐ڐ��̂����ŁC�X����m�ɓ������ڐ��̕������� (2) �o�Ȑ� �̐ڐ��̂����ŁC�X����m�ɓ������ڐ��̕������� �̐ڐ��̂����ŁC�X����m�ɓ������ڐ��̕������� (3) ������ �̐ڐ��̂����ŁC�X����m (��0)�ɓ������ڐ��̕������� |
�i�ؖ��j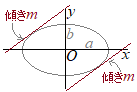 (1)��
(1)�����߂�ڐ��̕������� ��x���W�ɂ��ďd�������悤�ɁC���ʎ��ɂ���D=0�ƂȂ���������߂�Ƃ悢�D (2)��(1)�ɑ������� ������ |
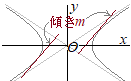 (2a)��
(2a)�����߂�ڐ��̕������� ��x���W�ɂ��ďd�������悤�ɁC���ʎ��ɂ���D=0�ƂȂ���������߂�Ƃ悢�D (4)��(3)�ɑ�������
�����ŁC\(a^2m^2-b^2=0\)�̂Ƃ��́C\(x\)�̂P���������ƂȂ��āC�d���������Ȃ��Ȃ邩��C\(a^2m^2-b^2\ne 0\)�̏ꍇ���l����D
������
�����ŁC\(a^2m^2-b^2\lt 0\)�̂Ƃ��́C\(k\)�������łȂ��Ȃ邩��C\(a^2m^2-b^2\gt 0\)�������ƂȂ�D���Ȃ킿�C\(\displaystyle\mid m\mid\gt\mid\frac{b}{a}\mid\)�̏ꍇ�����ڐ������܂�D
(2b)���C���l�ɂ��ďؖ��ł���D
|
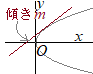 (3)��
(3)�����߂�ڐ��̕������� ��x���W�ɂ��ďd�������悤�ɁC���ʎ��ɂ���D=0�ƂȂ���������߂�Ƃ悢�D (6)��(5)�ɑ������� ������ |
|
�y���1.1�z
�i�j�@�ȉ~ ����(1)�� ���������o���Ă��Ȃ��Ă��C���ʎ����g���Ď����Ōv�Z����ΐ����łł���D |
�y���1.2�z
�@�ȉ~ 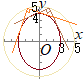 �i�j
�i�j�����藧�D�@�����Q��m�̒l���Cm1, m2�Ƃ���ƁCm1, m2�́Cm�Ɋւ���Q�������� �̂Q�̉��ɂȂ�D �A�����قȂ�Q�̎�����m1, m2�����Ƃ��C���ƌW���̊W���� �A�j���W���ɕ��s�Ȑڐ�������Ƃ��́C�ڐ��̕������́C �C�j���W���ɕ��s�Ȑڐ��ł͂Ȃ��Ƃ��C��_��x���W��x��±3 �A�j�̓C�j�̉~���x=±3�ƂȂ鏜�O�_�߂Ă��邩��C���ǁC |
|
�y���1.3�z
�@�ȉ~ 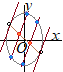 �i�j
�i�j�@�A�������� ���قȂ�Q�̎����������悤�ɁC��_��x���W�̔��ʎ��ɂ���D>0�Ƃ���D �@(2)��(1)�ɑ������� �@�قȂ�Q�_�Ō����̂� �@���̂Ƃ��C�Q��_�̍��W�� (5)(6)���狁�߂�O�Ղ̕������� �������C(4)����C �͈̔ͥ���i���j |
�y���1.4�z
�@�_(3, 4)����ȉ~ 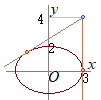 �i�j
�i�j�@�ړ_(3, 0)�Őڂ���ڐ�x=3�͑�ӂɓK����D �@x���ɐ����łȂ��ڐ��̕��������C(1)���g���āC ���߂�ڐ��̕������� �@�����̂����ŁC |
|
�y���1.5�z
�@�ȉ~ 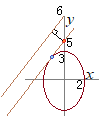 �i�j
�i�j�X��2�őȉ~ �̂���ċ��߂�� �ƂȂ邩��C�ŏ��l�� |
�y���2.1�z
�@�o�Ȑ� 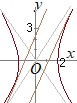 �i�j
�i�j����(2a)���g���� |
|
�y���2.2�z
�i�j�@�o�Ȑ� �@�A�������� �������������悤�ɁC���ʎ���p����k�̒l�͈̔͂����߂�D �@(2)��(1)�ɑ������� |
�y���2.3�z
�@�_(2, 4)����o�Ȑ� 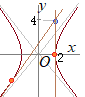 �i�j
�i�j�@�܂��Cx���ɐ����Ȓ���x=2���ڐ��ł��邱�Ƃ����炩�D �@����ȊO��y=mx+k�̌`�̐ڐ��́C����(2a)���� �Ə�����D���̐ڐ����C�_(2, 4)��ʂ邩�� �A�j �̗��ӂ��Q�悷��� �ƂȂ��āC���������Ȃ� �C�j ( �̗��ӂ��Q�悷��� �ƂȂ��āC�����ɓK����D �ȏォ��C |
|
�i�ʉ��j �ړ_�̍��W��(s, t)�Ƃ����ƁC�ڐ��̕������� ���̒������_(2, 4)��ʂ邩�� �܂��C(s, t)�͑o�Ȑ���ɂ��邩�� (2)(3)��A���������Ƃ��ĉ����Ɓm�r���o�߂͊e���Ŋm���߂Ă��������n ������(1)�ɖ߂��� |
�y���2.4�z
�@�o�Ȑ� 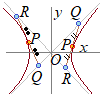 �i�j
�i�j�@�ړ_��P(s, t)�Ƃ����ƁC�ڐ��̕������� �������C�ړ_P(s, t)�͑o�Ȑ���ɂ��邩�� �����藧�D �@(1)�ƑQ�ߐ��̕����� �Ƃ̌�_�̍��W�����߂�D (1)(3)���� (3)��(1)�ɑ�� ��� (2’�j�ɂ�蕪���0�ɂȂ�Ȃ��D �����Q��x���W�Ƃ���D ���l�ɂ��āC(1)(4)���� (4)��(1)�ɑ�� ��� (2’�j�ɂ�蕪���0�ɂȂ�Ȃ��D �����R��x���W�Ƃ���D (5)(6)����Q, R�̒��_��x���W�����߂�� �Ƃ���ŁC(2’)���� ������C���� �����藧�D�����ł��邩��CQ, R�̒��_��x���W��P��x���W�ɓ�������Cy���W�ɂ��Ă����藧�D �@�ȏ�ɂ��CPQ=PR�����藧�D����ؖ��I��
���̖��ł́C�o�Ȑ�
|
|
�y���2.5�z
�@�o�Ȑ� 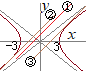 �i�j
�i�j����(4.2a)�ɂ��C �i�����͉E�}�̇A�B�ɑΉ�����j �E�}�@�ɑΉ����钼��y=x+1����A�܂��͇B�܂ł̍ŒZ���������߂�Ƃ悢���C�A�̕����Z���D �����ŁCy=x+1��̓K���ȂP�_�C�Ⴆ��(0, 1)���璼�� |
�y���3.1�z
�i�j�@������ ����(3)�ɂ����āCp=2, m=2�Ƃ���� |
|
�y���3.2�z
�i�j�@������ ���߂�ڐ��̕������� ��x���W�ɂ��ďd�������悤�ɁC���ʎ��ɂ���D=0�ƂȂ���������߂�Ƃ悢�D (2)��(1)�ɑ������� \( \displaystyle x^2=8(2x+k) \) \( \displaystyle x^2-16x-8k=0 \) \( \displaystyle D'=64+8k=0 \) \( \displaystyle k=-8 \) ���������� \( \displaystyle y=2x-8 \)����i���j |
�y���3.3�z
�@������ 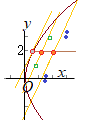 �i�j
�i�j�@�A�������� ���قȂ�Q�̎����������悤�ɁC���ʎ���p����k�̒l�͈̔͂����߂�D �@�܂��C���̂Ƃ��C���ƌW���̊W��p���āC�Q��_�̒��_�̍��W�����߂�D �@(2)��(1)�ɑ������ (3)�ɂ��āC���ʎ������ƂȂ������ �@�܂��C(3)�ɂ��āC���ƌW���̊W����C�Q��_�̒��_�̍��W�� �@�Ȃ��C(4)(5)����C �@�ȏ�ɂ��C |