|
■放物線 ■1 放物線の方程式の標準形 ※ 放物線の方程式は,中学校と高校数学Iで2次関数のグラフとして習う. ■ 方程式
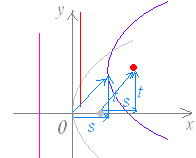
で表わされる曲線は,右図1のような放物線になる. ○ (1)を放物線の方程式の標準形という. ○ この曲線は「定点 F(p , 0) と定直線 x=−p からの距離が等しい点の軌跡」となっている.(解説は次の項目↓) ○ 点 F(p , 0) を放物線の焦点といい,直線 x=−p を準線という. ○ 点 O(0 , 0) を放物線の頂点という. ○ (1)の放物線は x 軸に関して対称となっている. この対称軸を放物線の軸という.すなわち,軸の方程式は ■ (1)において x , y の役割を入れ換えたもの このとき,焦点は y 軸上にあり,焦点の座標は |
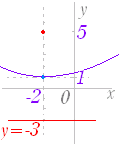
※ 高校数学Iで習う放物線のグラフ
図1
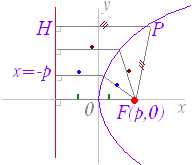 図2 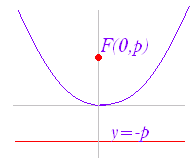 |
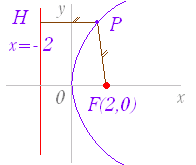
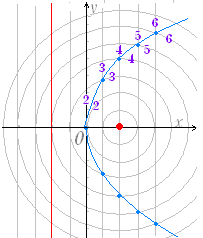
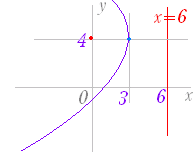
| 《基本事項のチェック》 y2=8x は,右図3のような形の放物線で, y2=4·2·x と変形すると,p=2 となるから, 焦点の座標は F(2 , 0) 準線の方程式は x=−2 頂点の座標は (0 , 0) 放物線上の任意の1点を P とするとき,FP = HP となる. |
図3
 |
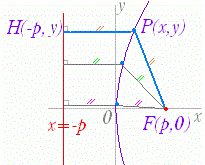
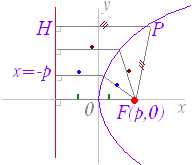 【要点1】横向きの場合
【要点1】横向きの場合放物線
焦点の座標は
である.準線の方程式は このとき,動点 動点から準線に引いた垂線の長さ について すなわち が成り立つ |
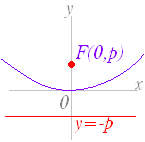
 【要点2】縦向きの場合
【要点2】縦向きの場合放物線
焦点の座標は
である.準線の方程式は このとき,動点 動点から準線に引いた垂線の長さ について すなわち が成り立つ |
| 問題 |
→閉じる←
(1) 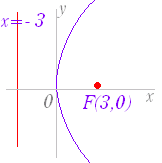 p=3 だから, 焦点は x 軸上にあり,F(3 , 0) 準線の方程式は x=−3 (2) 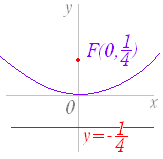 x2=4··y と変形すると,p= だから
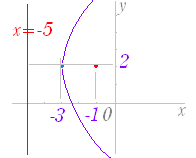
x2=4··y と変形すると,p= だから焦点は y 軸上にあり,(0 , ) 準線の方程式は y=− (3) 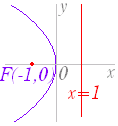 y2=4·(−1)·x と変形すると,p=−1 だから 焦点は x 軸上にあり,(- 1 , 0 ) 準線の方程式は x=1 |
 移動後の方程式は
移動後の方程式は