|
■1 楕円の方程式の標準形 ■ a>b>0 のとき,方程式
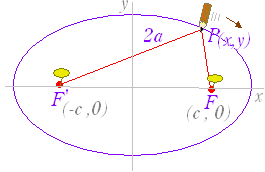
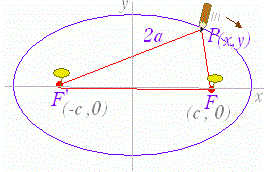
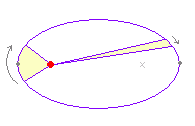
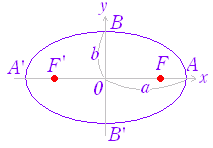
+=1 …(1) で表わされる曲線は,右図1のような楕円になる. ○ (1)を楕円の方程式の標準形という. ○ この曲線は「2定点 F( , 0) , F’(− , 0) からの距離の和が一定 2a である点の軌跡」となっている. ○ 2点 F( , 0) , F’(− , 0) を楕円の焦点という. ○ 点 A(a , 0) , A’(−a, 0) , B(0 , b) , B’(0, −b) を頂点という. ○ 線分 AA’ を長軸,線分 BB’ を短軸という.(※円で言えば半径ではなく直径に相等するものが,長軸・短軸なので,(1)の楕円の長軸の長さは 2a,短軸の長さは 2b となる.) ○ 長軸と短軸の交点を中心という.(1)の楕円の中心は原点 O( 0 , 0 ) にある. ■ b>a>0 のときは,右図2のような楕円になる. このとき,焦点は y 軸上にあり,焦点の座標は F(0 , ) , F’(0 , − ) また,長軸は y軸上にあり,その長さは 2b ,短軸は x 軸上にあり,その長さは 2a となる. |
図1
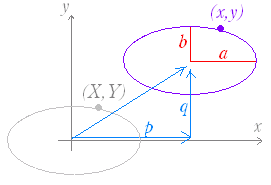
○ 以下の考え方において,三平方の定理(ピタゴラスの定理)を用いて「 a , b から c を求める」「 a , c から b を求める」計算がつねに登場し,この図が鍵となる.(図の意味は,■2で述べる.)
図2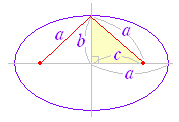 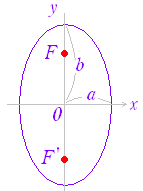 |
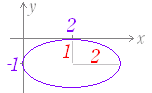
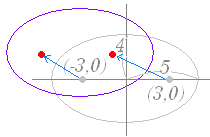
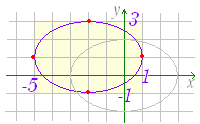
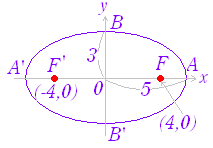
| 《基本事項のチェック》 +=1 は,右図3のような形の楕円で, 焦点の座標は F(4 , 0) , F’(−4 , 0), 長軸の長さは 10,短軸の長さは 6 頂点の座標は (5 , 0) , (−5 , 0) , (0 , 3) , (0 ,−3), 中心の座標は (0 , 0) である. 楕円上の任意の1点を P とするとき,FP+F’P=10 となる. |
図3
 |
|
※理論を理解するよりも,「公式のあてはめ」の方が具体的に取りかかりやすいので,ここでは先に「公式のあてはめ」を練習し,その後で理論の理解に進むことにします.
問題
|
→閉じる←
(1) a=5 , b=4 だから,=3 a>b だから(横長になり)焦点は x 軸上にあり,(±3 , 0) 長軸の長さは 2a=10,短軸の長さは 2b=8 (2) a=2 , b=3 だから,= b>a だから(縦長になり)焦点は y 軸上にあり,(0 , ±) 長軸の長さは 2b=6,短軸の長さは 2a=4 (3) +=1 と変形すると, a=2 , b=1 だから,= a>b だから(横長になり)焦点は x 軸上にあり,(± ,0 ) 長軸の長さは 2a=4,短軸の長さは 2b=2 |