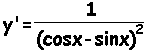← PC用は別頁
|
*** 科目 *** 数Ⅰ・A数Ⅱ・B数Ⅲ高卒・大学初年度 *** 単元 *** 複素数平面二次曲線媒介変数表示と極座標 数列の極限関数導関数不定積分定積分 行列1次変換 ※高校数学Ⅲの「微分・導関数」について,このサイトには次の教材があります.
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は,他の頁を見てください. が現在地です. ↓微分係数,連続,微分可能 ↓積の微分 ↓商,分数関数の微分 ↓合成関数の微分 ↓無理関数の微分 ↓媒介変数表示のときの微分法 ↓同(2) ↓陰関数の微分法 ↓重要な極限値(1)_三角関数 ↓三角関数の微分-現在地 ↓三角関数の微分(2) ↓指数関数,対数関数の微分 ↓対数微分法 ↓微分(総合演習) ↓漸近線の方程式 ↓同(2) ↓凹凸と変曲点 ↓総合--増減.極値.凹凸.変曲点.漸近線(1) ↓分数関数の増減.極値.漸近線 グラフの概形と漸近線(一覧) |
 不定形の極限
不定形の極限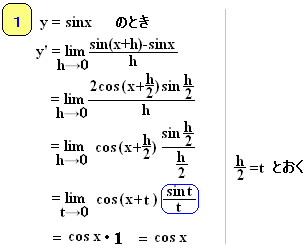
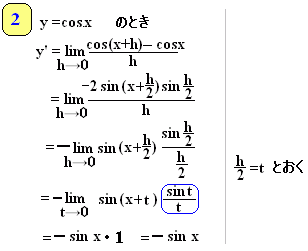
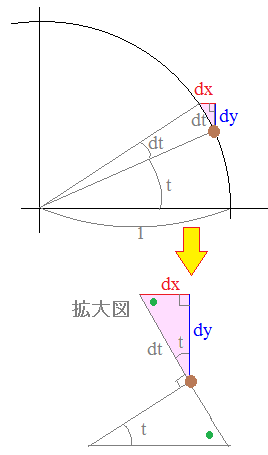 (参考)
(参考)
 ・・答
・・答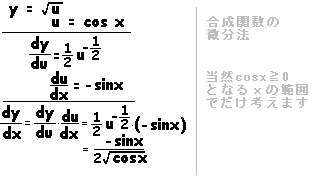 ・・答
・・答