|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
���͂��߂Ɂ�…���̕ł��w�K����ƁA�����ł���悤�ɂȂ�̂�
���O�����̒藝�̊g��…�i���w�Z�̐��w�Ƃ̊W�j
 �@�ł́A�}2�̂悤����A��90���łȂ��Ƃ��ɂ́A���̒藝�͂ǂ�Ȍ`�ɂȂ�̂ł��傤���B 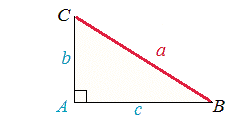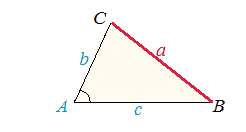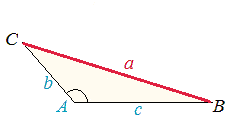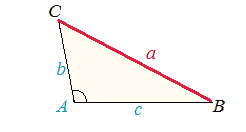
���O�p�`�̍��������E��������Ƃ̊W…�i���w�Z�̐��w�Ƃ̊W�j
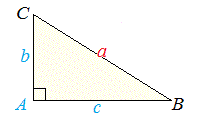
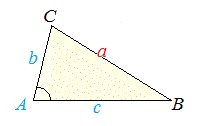 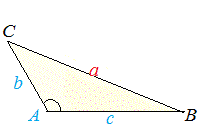 �@���̕ł��w�K����ƁA��Ӂib , c�j�Ƃ��̊Ԃ̊p�iA�j�����3�̕Ӂia�j�̒������v�Z�ŋ��߂邱�Ƃ��ł���悤�ɂȂ�܂��B 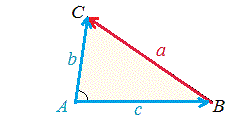 �@�O�p�`�̍��������E��������ɂ́A���̑��u3�ӂ��^������ƎO�p�`�͌��܂�v�Ƃ����̂�����܂��B �@����ɂ��A3�ӂ̒������^������A3�̊p�x�����ׂČ��܂�͂��ł��̂ŁA�u3�ӂ̒����v���u3�̊p�̑傫���v�Ƃ����v�Z���ł���͂��ɂȂ�܂��B �@���̕ł��w�K����ƁA�u3�ӂ̒����v����u3�̊p�̑傫���v���v�Z���邱�Ƃ��ł���悤�ɂȂ�܂��B
�i�Q�l�j
�@�]���藝�ɂ����āA��A>90���̂Ƃ� �@�Ⴆ�A��́y��1�z�ɂ�����A=120���̂Ƃ��AcosA=−1/2�ɂȂ�܂��̂ŁA �@a2=52+32−2�~5�~3�~ (−1/2) �@�@�@=52+32+15 |
���̃y�[�W�̃}�C�i�[�`�F���W����J�o�[�Ńy�[�W
***���P***�@�]���藝�i�O�[�O���u���K�[�Łj�́C�������
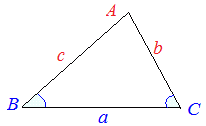
�@��ABC�ɂ��Ď��̊W�������藧���܂��B
�� (A)�����o����悭�A�c��2�͂��݂��̊W���番����܂��B
�y��1�z
b=5, c=3 , A=120���̂Ƃ��Aa�����߂�ɂ� a2=52+32−2�~5�~3�~ cos120��=49 a=7 (>0) …�i���j
�y�]���藝(A)�̏ؖ��z
b, c , A���^�����Ă���Ƃ��A���p�O�p�`AHC��3�ӂ̒��������܂�̂ŁAHB , HC�̒l����O�����̒藝���g����
BC�����߂܂��B
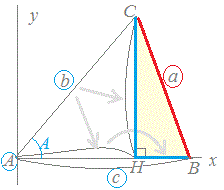 �@��AHC�͒��p�O�p�`������A �@�@ 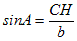 �@�� CH=b sinA �@�� CH=b sinA�@�@ 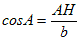 �@�� AH=b cosA �� BH=c−b cosA �@�� AH=b cosA �� BH=c−b cosA�@��BCH�͒��p�O�p�`������A�O�����̒藝�ɂ�� �@�@a2=(b sinA)2+(c−b cosA)2 �@�@�@=b2sin2A+c2−2bc cosA+b2cos2A �@�@�@=b2(sin2A+cos2A)+c2−2bc cosA �@�@�@=b2+c2−2bc cosA ��A��90�������傫���Ƃ��́A��̏ؖ���cosA<0�ƂȂ邪���l�ɂ��Ď������Ƃ��ł��܂��B�܂��A��A=90���̂Ƃ��́AcosA=0�ƂȂ�A�O�����̒藝�ɂ��a2=b2+c2�����藧���܂��B�� (B)(C)�ɂ��Ă����l�ɂ��Ď�����܂��B |
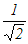
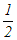
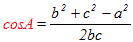
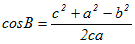 …(B’)
…(B’)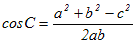 …(C’)
…(C’)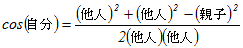
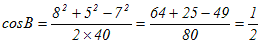
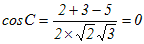
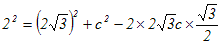
 (1)(2)�́A��ɏq�ׂ��悤�Ɂi�͂��߂̈���́j�]���藝�ʼn������Ƃ��ł��܂��B
(1)(2)�́A��ɏq�ׂ��悤�Ɂi�͂��߂̈���́j�]���藝�ʼn������Ƃ��ł��܂��B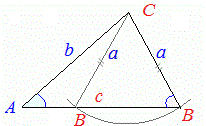 �i�Q�l�j
�i�Q�l�j