|
■ 正弦定理・余弦定理 ◇公式要約◇ ［正弦定理］ △ABC の外接円の半径をR とするとき， ===2R ［余弦定理］ ［三角形の面積］ △ABC の面積をS とするとき， S=absinC=bcsinA=casinB ※ センター試験では，これらの公式をそのまま適用すれば解ける問題が多く出されている． ただし，根号計算が含まれている他，右の関係もよく使われている． |
※ 円に内接する四辺形の向かい合う角の和は180°だから，次の図においてB+D=180°，sinB=sinD となり， △ABC:△CDA =AB·BCsinB : CD·DAsinD =AB·BC : CD·DA また，ACを共通の底辺と見ると△ABC と△CDA の高さの比は，BP : PD に等しいから △ABC:△CDA=BP : PD 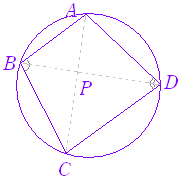 ※ 余弦定理において，２辺とその間にない角が与えられた場合は，（次の形で未知数を a として）２次方程式を解き，２つの解のうち適するものを選べばよい．  |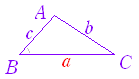
...メニューに戻る