正弦定理

→ 携帯版は別頁

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック

◎内側の色を変えるには，次の色をクリック

◎標準文字色を変えるには，次の色をクリック

== 正弦定理（問題） ==

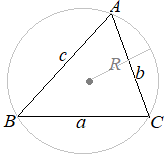
三角形の辺と角の名前の付け方

　右図のような△ABCがあるとき
(1) 頂点の名前A, B, Cを使ってその内角の大きさを表す．

　例えば，角Aとは∠CABのことを表す．

(2) 各頂点の対辺の長さを対応する小文字で表す．

　例えば，角Aの対辺の長さをBC=aとする．

正弦定理

△ABCの外接円の半径をRとするとき
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つ．

正弦定理を使って三角形の辺や角を求める方法

(1) 辺の長さと角の大きさが１組分かっていれば，外接円の半径が求められる．

　例えば，Aとaが分かっていれば，外接円の半径Rが求められる．
$\frac{a}{\sin A}=2R$

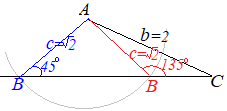
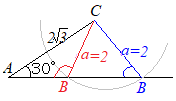
(2) a, A, Bのように１組の辺角(a, A)と他の１つの角(B)が分かっていれば，辺bが求められる．
$\frac{a}{\sin A}=\frac{b}{\sin B}\rightarrow b=\frac{a\sin B}{\sin A}$
(3) a, A, bのように１組の辺角(a, A)と他の１つの辺(b)が分かっていれば，角Bが求められる．
$\frac{a}{\sin A}=\frac{b}{\sin B}\rightarrow \sin B=\frac{b\sin A}{a}$
※(3)では一般に角度が２つ求まる可能性があるが，Aと足すと180°以上になる角Bは解にならない．（Cが負になって三角形が描けない）

このページのマイナーチェンジありカバー版ページ
（グーグルブロガー版）は，こちら⇒

次のような作戦盤を書いて，「上下1組がそろっていれば」正弦定理が使える（Bを攻める）

a	b	c
A	B	C

角が２つ求まると３つ目はただ同然（中学の数学）：C=180°−(A+B)は「ただ」で手に入る

a	b	c
A	B	C

「上下1組がそろった」a, A（b, Bでもよい）と角Cを使って辺cを攻める
　結局，3つの辺と3つの角が全部分かる．［陣取りゲーム完了！］

【問題１】　（選択肢の中から正しいものをクリック）

(1)
△ABCにおいて， $a=3,\hspace{5}A=120^{\circ}$ のとき，外接円の半径Rを求めてください．

…（途中経過）…
$\frac{3}{\sin 120^{\circ}}=2R$ に $\sin 120^{\circ}=\frac{\sqrt{3}}{2}$ を代入すると
$\frac{3}{\frac{\sqrt{3}}{2}}=2R$

左辺を
$3\div\frac{\sqrt{3}}{2}=3\times\frac{2}{\sqrt{3}}$
と変形してもよい

左辺の分母分子に２を掛けると
$\frac{6}{\sqrt{3}}=2R$
$R=\frac{6}{2\sqrt{3}}=\hspace{3}\cdots$

解説やり直す

…（解答の選択肢）…

$2$ $\sqrt{3}$ $3$ $\sqrt{6}$

$R=\frac{6}{2\sqrt{3}}=\frac{6\times \sqrt{3}}{2\sqrt{3}\times \sqrt{3}}=\frac{6\sqrt{3}}{6}=\sqrt{3}$ …（答）

→閉じる←

(2)
△ABCにおいて， $a=8,\hspace{5}A=45^{\circ},\hspace{5}B=60^{\circ}$ のとき，bを求めてください．

…（途中経過）…
$\frac{8}{\sin 45^{\circ}}=\frac{b}{\sin 60^{\circ}}$ に $\sin 45^{\circ}=\frac{1}{\sqrt{2}},\hspace{5}\sin 60^{\circ}=\frac{\sqrt{3}}{2}$ を代入すると
$\frac{8}{\frac{1}{\sqrt{2}}}=\frac{b}{\frac{\sqrt{3}}{2}}$

左辺を
$8\div\frac{1}{\sqrt{2}}=8\times\frac{\sqrt{2}}{1}$
と変形してもよい

左辺の分母分子に $\sqrt{2}$ を掛けると
$8\sqrt{2}$

右辺を
$b\div\frac{\sqrt{3}}{2}=b\times\frac{2}{\sqrt{3}}$
と変形してもよい

右辺の分母分子に2を掛けると
$\frac{2b}{\sqrt{3}}$
方程式は
$8\sqrt{2}=\frac{2b}{\sqrt{3}}\hspace{10}\rightarrow\hspace{10}b=8\sqrt{2}\times\frac{\sqrt{3}}{2}=\hspace{3}\cdots$

解説やり直す

…（解答の選択肢）…

$2\sqrt{3}$ $4\sqrt{3}$ $2\sqrt{6}$ $4\sqrt{6}$

$b=8\sqrt{2}\times\frac{\sqrt{3}}{2}=4\sqrt{6}$ …（答）

→閉じる←

(3)
△ABCにおいて， $a=\sqrt{6},\hspace{5}A=45^{\circ},\hspace{5}b=\sqrt{3}$ のとき，Bを求めてください．

…（途中経過）…
$\frac{\sqrt{6}}{\sin 45^{\circ}}=\frac{\sqrt{3}}{\sin B}$ に $\sin 45^{\circ}=\frac{1}{\sqrt{2}}$ を代入すると
$\frac{\sqrt{6}}{\frac{1}{\sqrt{2}}}=\frac{\sqrt{3}}{\sin B}$
$\sin B=\frac{\sqrt{3}}{\sqrt{6}}\times\frac{1}{\sqrt{2}}=\frac{1}{2}$
ここから，B=30°, 150°のどちらが答か，両方とも答かと考えます

解説やり直す

…（解答の選択肢）…

30° 150° 30°と150°

A=45°, B=150°の組は三角形ができない
（A+B>180°だからA+B+C=180°にできない）
A=45°, B=30°の組は三角形ができる．
したがって，B=30° …（答）

→閉じる←

(4)
△ABCにおいて， $b=2,\hspace{5}c=\sqrt{2},\hspace{5}C=30^{\circ}$ のとき，Bを求めてください．

…（途中経過）…
$\frac{2}{\sin B}=\frac{\sqrt{2}}{\sin 30^{\circ}}$ に $\sin 30^{\circ}=\frac{1}{2}$ を代入すると
$\frac{2}{\sin B}=\frac{\sqrt{2}}{\frac{1}{2}}$
$\sin B=\frac{2}{\sqrt{2}}\times\frac{1}{2}=\frac{1}{\sqrt{2}}$
ここから，B=45°, 135°のどちらが答か，両方とも答かと考えます

解説やり直す

…（解答の選択肢）…

45° 135° 45°と135°

B=45°, C=30°の組は三角形ができる
B+C=75°だからA=105°になる）
B=135°, C=30°の組も三角形ができる．
B+C=165°だからA=15°になる）
したがって，B=45°とB=135°の両方 …（答）

※b, c, Cが与えられた三角形は，２辺とその間にない角が与えられており，三角形の決定条件を満たしていません．右図のように，∠C=30°として，Ａを中心に半径 $c=\sqrt{2}$ の円を描くと底辺とは２か所で交わり，どちらも三角形になります

→閉じる←

※最初のヒントが見えない問題です．計算用紙を使って，よく考えてから答えてください．
【問題２】　（選択肢の中から正しいものをクリック）

(1)
△ABCにおいて，a=8, A=45°のとき，外接円の半径Rを求めてください．

解説やり直す

$2$ $4\sqrt{3}$ $4\sqrt{2}$ $8\sqrt{2}$

$\frac{8}{\sin 45^{\circ}}=2R$
より
$\frac{8}{\frac{1}{\sqrt{2}}}=2R$
$R=\frac{8\sqrt{2}}{2}=4\sqrt{2}$ …（答）

→閉じる←

(2)
△ABCにおいて，b=6, A=45°, B=30°のとき，aを求めてください．

解説やり直す

$6\sqrt{2}$ $6\sqrt{3}$ $12\sqrt{3}$ $12\sqrt{6}$

$\frac{a}{\sin 45^{\circ}}=\frac{6}{\sin 30^{\circ}}$
より
$a=\frac{6\sin 45^{\circ}}{\sin 30^{\circ}}=\frac{6\times\frac{1}{\sqrt{2}}}{\frac{1}{2}}=6\times\frac{1}{\sqrt{2}}\times 2$
$=6\sqrt{2}$ …（答）

→閉じる←

(3)
△ABCにおいて， $a=2,\hspace{5}b=2\sqrt{3},\hspace{5}A=30^{\circ}$ のとき，Bを求めてください．

解説やり直す

60° 120° 60°と120°

$\frac{2}{\sin 30^{\circ}}=\frac{2\sqrt{3}}{\sin B}$
より
$\sin B=\frac{2\sqrt{3}\sin 30^{\circ}}{2}=\frac{\sqrt{3}}{2}$
B=60°, 120°…(答)

※a, b, Aが与えられた三角形は，２辺とその間にない角が与えられており，三角形の決定条件を満たしていません．右図のように，∠A=30°として，Cを中心に半径2の円を描くと底辺とは２か所で交わり，どちらも三角形になります

→閉じる←

(4)
△ABCにおいて，a=10, B=60°, C=75°のとき，bを求めてください．

解説やり直す

$2\sqrt{6}$ $5\sqrt{6}$ $10\sqrt{3}$ $10\sqrt{6}$

※a, B, Cのように既知の辺角が１組もないときは，そのままでは正弦定理を使えません．
初めに，A=180°−(B+C)によりAを求めておきます．
A=180°−(B+C)=45°
$\frac{10}{\sin 45^{\circ}}=\frac{b}{\sin 60^{\circ}}$
$b=\frac{10\sin 60^{\circ}}{\sin 45^{\circ}}=\frac{10\times\frac{\sqrt{3}}{2}}{\frac{1}{\sqrt{2}}}=10\times\frac{\sqrt{3}}{2}\times\frac{\sqrt{2}}{1}=5\sqrt{6}$ …(答)

→閉じる←

...メニューに戻る