5. 次のような関係式も成り立つ
△ABCの三辺の長さを a,b,cとし,  \( s=\dfrac{a+ b+ c}{2} \) \( s=\dfrac{a+ b+ c}{2} \)とおくと,
 \( \color{blue}{\cos A+\cos B+\cos C=1+\dfrac{r}{R}} \)・・・(5.1) \( \color{blue}{\cos A+\cos B+\cos C=1+\dfrac{r}{R}} \)・・・(5.1)
&chco=0000ff) \( \color{blue}{a\cot A+ b\cot B+ c\cot C=2(R+r)} \)・・・(5.2) \( \color{blue}{a\cot A+ b\cot B+ c\cot C=2(R+r)} \)・・・(5.2)
(証明)
|
■==以下の式を,高校生が覚える必要はないが,大学入試問題として出題されることはある==■
6. 円に内接する四辺形の辺の長さa, b, c, dとするとき,この四辺形の面積を表す次の公式を「ブラーマグプタの公式」という
(ブラーマグプタ:インドの数学者,598〜660年.--日本では聖徳太子の時代に,インドでこんな公式を考えた人がいた!!--.なお,ブラーマグプタ自身は一般の四辺形の面積を求めているつもりであったが,この公式は円に内接する四辺形の場合にのみ成り立つ)
円に内接する四辺形 ABCDの辺の長さを各々 a, b, c, dとし,  \( s=\dfrac{a+ b+ c+ d}{2} \) \( s=\dfrac{a+ b+ c+ d}{2} \)とおくと
● 四辺形 ABCDの面積 Sは
(s-b)(s-c)(s-d)}&chco=0000ff) \( \color{blue}{S=\sqrt{(s-a)(s-b)(s-c)(s-d)}} \)・・・(6.1) \( \color{blue}{S=\sqrt{(s-a)(s-b)(s-c)(s-d)}} \)・・・(6.1)
● 対角線 ACの長さを l,対角線 BDの長さを l’とおくと
(ac%2B bd)}{ab%2B cd}}&chco=0000ff) \( \color{blue}{ l=\sqrt{ \dfrac{(ad+ bc)(ac+ bd)}{ab+cd} } } \)・・・(6.2) \( \color{blue}{ l=\sqrt{ \dfrac{(ad+ bc)(ac+ bd)}{ab+cd} } } \)・・・(6.2)
(ac%2B bd)}{ad%2B bc}}&chco=0000ff) \( \color{blue}{ l'=\sqrt{\dfrac{(ab+ cd)(ac+ bd)}{ad+ bc}} } \)・・・(6.3) \( \color{blue}{ l'=\sqrt{\dfrac{(ab+ cd)(ac+ bd)}{ad+ bc}} } \)・・・(6.3)
● 対角線のなす角を θとおくと
(s-b)(s-c)(s-d)}}{ac%2B bd}&chco=0000ff) \( \color{blue}{ \sin\theta\!=\!\dfrac{2\sqrt{(s\!-\!a)(s\!-\!b)(s\!-\!c)(s\!-\!d)}}{ac+ bd} } \)・・・(6.4) \( \color{blue}{ \sin\theta\!=\!\dfrac{2\sqrt{(s\!-\!a)(s\!-\!b)(s\!-\!c)(s\!-\!d)}}{ac+ bd} } \)・・・(6.4)
● 内接四辺形の角は
}&chco=0000ff) \( \color{blue}{ \cos A=\dfrac{a^2+ d^2-b^2-c^2}{2(ad+ bc)} } \)・・・(6.5) \( \color{blue}{ \cos A=\dfrac{a^2+ d^2-b^2-c^2}{2(ad+ bc)} } \)・・・(6.5)
(B,C,Dについても同様)
● 外接円の半径は
(ad%2B bc)(ac%2B bd)}{(s-a)(s-b)(s-c)(s-d)}}&chco=0000ff) \( \color{blue}{ R=\dfrac{1}{4}\sqrt{\dfrac{(ab+ cd)(ad+ bc)(ac+ bd)}{(s-a)(s-b)(s-c)(s-d)}} } \)・・・(6.6) \( \color{blue}{ R=\dfrac{1}{4}\sqrt{\dfrac{(ab+ cd)(ad+ bc)(ac+ bd)}{(s-a)(s-b)(s-c)(s-d)}} } \)・・・(6.6)
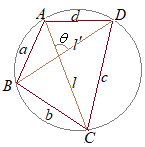 右図において,四辺形を2つの△ABDと△BCDに分けて,それらの面積の和を求める.
右図において,四辺形を2つの△ABDと△BCDに分けて,それらの面積の和を求める.
 \( S=\dfrac{1}{2}ad\sin A+\dfrac{1}{2}bc\sin C \) \( S=\dfrac{1}{2}ad\sin A+\dfrac{1}{2}bc\sin C \)
この四辺形は円に内接しているから
 \( A+ C=180^{\circ} \) \( A+ C=180^{\circ} \)
 \( C=180^{\circ}-A \)・・・(*1) \( C=180^{\circ}-A \)・・・(*1)
 \( \sin C=\sin A \) \( \sin C=\sin A \)
したがって
\sin A) \( S=\dfrac{1}{2}(ad+bc)\sin A \)・・・(*2) \( S=\dfrac{1}{2}(ad+bc)\sin A \)・・・(*2)
△ABDと△BCDについて、余弦定理を用いると
 \( \cos A=\dfrac{a^2+ d^2-l'^2}{2ad} \)・・・(*3) \( \cos A=\dfrac{a^2+ d^2-l'^2}{2ad} \)・・・(*3)
 \( \cos C=\dfrac{b^2+ c^2-l'^2}{2bc} \)・・・(*4) \( \cos C=\dfrac{b^2+ c^2-l'^2}{2bc} \)・・・(*4)
(*1)により(*4)は,次の形に書ける
 \( \cos A=\dfrac{-b^2-c^2+ l'^2}{2bc} \)・・・(*4’) \( \cos A=\dfrac{-b^2-c^2+ l'^2}{2bc} \)・・・(*4’)
|
 右図において,四辺形を2つの
右図において,四辺形を2つの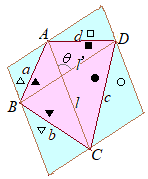 対角線
対角線