■放物線の移動 (はじめに)
(はじめに)
一般的には,グラフの移動は,グラフ上の各点の移動をもとにした「座標変換」で求めることができます.すなわち,グラフ上の各点を移動してできる新しい点を結んだものが新しいグラフです.
しかし,このように一般的に行うのは考え方や計算が難しくなるので,高等学校の数学Iでは「座標変換」をもとにした方法でなく,もっと簡単な「放物線の頂点の移動」をもとにした方法で解くのが普通です. この頁では,与えられた放物線を移動してできる新しい放物線の方程式を求めるための「座標変換」による方法と「頂点の移動」による方法を紹介しますが,最終的には「頂点の移動」による方法で解けるようになることを目指します. |
|
|
【グラフの平行移動:要点】
○[座標変換による方法]
(A) y=f(x)の形になっているとき
y=f(x)のグラフをx軸の正の向きにp,y軸の正の向きにqだけ平行移動してできるグラフの方程式は y=f(x−p)+q になる. 【例】 …高校1年では習わないものばかり
(1) 元のグラフの方程式:y=2x3
移動:x方向に1,y方向に4 新しいグラフの方程式:y=2(x−1)3+4
(2) 元のグラフの方程式:y=+3
移動:x方向に5,y方向に6 新しいグラフの方程式:y=+9
(3) 元のグラフの方程式:y=2+3
移動:x方向に4,y方向に−5 新しいグラフの方程式:y=2−2 (B) yについて解かれていないとき f(x, y)=0のグラフをx軸の正の向きにp,y軸の正の向きにqだけ平行移動してできるグラフの方程式は f(x−p, y−q)=0 になる. 【例】 …高校1年では習わないものばかり
(1) 元のグラフの方程式:x2+y2=1(円)
移動:x方向に2,y方向に3 新しいグラフの方程式:(x−2)2+(y−3)2=1
(2) 元のグラフの方程式:xy=−3(直角双曲線)
移動:x方向に−2,y方向に1 新しいグラフの方程式:(x+2)(y−1)=−3
(3) 元のグラフの方程式:4x=y2(横向きの放物線)
移動:x方向に1,y方向に−2 新しいグラフの方程式:4(x−1)=(y+2)2
≪この方法の強い所≫
…どんな形の関数に対しても使えること ≪この方法の弱い所≫ …高校1年生では難しいこと 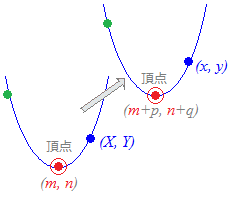 (解説)
(解説)(A) 元のグラフの方程式がy=f(x)であるときに,グラフ上の各点をx軸の正の向きにp,y軸の正の向きにqだけ平行移動してできるグラフの方程式は次のようにして求められる. 元の点(X, Y)はy=f(x)上にあるから,次の関係式を満たす
Y=f(X) …(1)
元の点(X, Y)をx軸の正の向きにp,y軸の正の向きにqだけ平行移動すると,新しい点(x, y)に移るのだから
x=X+p …(2)
新しいグラフの方程式とは,新しい点(x, y)の満たすべき関係式のことだから,(1)(2)を使って元の座標(X, Y)を消去すればよい.y=Y+q (2)より
X=x−p …(2’)
(2’)を(1)に代入するとY=y−q
y−q=f(x−p) …(3)
このままでもよいが,通常はyについて解かれた形が好まれるので,qを移項して,次の形で使う.
y=f(x−p)+q …(4)
(B) についても同様にして示せる.
f(x, y)=0 → f(x−p, y−q)=0 …(5)
 ≪よくある質問≫
≪よくある質問≫= = Q1.= = 例えばx方向に1,y方向に2だけ平行移動すると y=f(x−1)+2 となって,yは符号を変えなくてもそのまま使えるのに,xは符号を逆にしなければならないのは,不公平だ・・#yはずるい#という苦情について.
⇒そんなことはありません.実際,(3)でも(5)でも,右や上に移動するときに,増えずに逆にx−p, y−qになって,公平に泣かされています.(4)でyだけ見かけの符号のまま+qになっているのは,「yについて解かれた形が好まれる」という習慣に従って移項したためです.移項しなければ両方ともマイナスです.
= = Q2.= = 重要なのは,(2)では (新座標)=(旧座標)+○ となっている所を(2’)に変形するために (旧座標)=(新座標)−○ とする所です. 目を凝らしてよく見ると
y−q=f(x−p)
と Y=f(X)
X=x−p
Y=y−q だから は同じことを書いているのです. (B)の公式はf(x, y)=0 → f(x−p, y−q)=0となっているのに,右辺が0でないような x2+y2=1, xy=−3, 4x=y2に適用するのは反則ではないのか##
⇒移項すれば直ちにx2+y2−1=0, xy+3=0, 4x−y2=0となるので,説明なしで使っています.

【問題3】
y=−2(x−3)2+4のグラフを,どちら向きに幾ら平行移動すればy=−2(x+1)2+6のグラフにちょうど重なりますか. 1x軸の正の向きに−4,y軸の正の向きに−2 2x軸の正の向きに−4,y軸の正の向きに2 3x軸の正の向きに4,y軸の正の向きに−2 4x軸の正の向きに4,y軸の正の向きに2 解説
形は同じで,頂点のx座標を3→−1にするには−4,y座標を4→6にするには+2.
したがって,x軸の正の向きに−4,y軸の正の向きに2だけ平行移動するとよい.
→2
|
○[頂点の移動による方法]
※ 高校数学Iでは,2次関数のグラフ(放物線)しか登場しないので,上記の弱点は気にならない.むしろ,頂点による移動は「放物線の移動の専属コーチ」だと考えるとよい.
(A) 元のグラフがy=ax2の形になっているとき
放物線y=ax2のグラフをx軸の正の向きにp,y軸の正の向きにqだけ平行移動してできるグラフの方程式は y=a(x−p)2+q になる. 【例】
(1) 元のグラフの方程式:y=2x2
移動:x方向に1,y方向に3 新しいグラフの方程式:y=2(x−1)2+3
(2) 元のグラフの方程式:y=3x2
移動:x方向に−1,y方向に4 新しいグラフの方程式:y=3(x+1)2+4
(3) 元のグラフの方程式:y=−x2
移動:x方向に2,y方向に−3 新しいグラフの方程式:y=−(x−2)2−3 (B) 元のグラフがy=a(x−m)2+nの形になっているとき 放物線y=a(x−m)2+nのグラフをx軸の正の向きにp,y軸の正の向きにqだけ平行移動してできるグラフの方程式は y=a(x−m−p)2+n+q になる. 【例】
(1) 元のグラフの方程式:y=3(x−1)2+2
移動:x方向に4,y方向に5 新しいグラフの方程式:y=3(x−5)2+7
(2) 元のグラフの方程式:y=2(x−1)2
移動:x方向に3,y方向に5 新しいグラフの方程式:y=2(x−4)2+5
(3) 元のグラフの方程式:y=−4x2+2
移動:x方向に3,y方向に−1 新しいグラフの方程式:y=−4(x−3)2+1
≪この方法の強い所≫
…放物線の移動が簡単にできること ≪この方法の弱い所≫ …放物線以外には使えないこと ※ 放物線(2次関数のグラフ)の移動で,注意すべきこととして
放物線の形(開き具合)はx2の係数aで決まるということです.
平行移動しても形は変わりませんので,x2の係数aは変わりません. y=ax2 → y=a(x−p)2+q 移動したときに変わるのは頂点の座標p, qだけです. 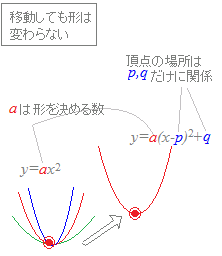
≪よくある質問≫
= = Q3.= = なぜ,x軸の正の向きにp,y軸の正の向きにq”だけ”平行移動というのか.”10円だけでは払えない”,”紙一重だけの差”のように,”たったそれっぽちの,ちょっとだけの”という意味か?
⇒違います.数学では,”ちょうどそれだけ”という意味を表すときに,”だけ”という用語がしばしが使われており,”少ない”という意味は含まれていません.
【問題1】
y=4x2のグラフを,x軸の正の向きに3,y軸の正の向きに−1だけ平行移動してできるグラフの方程式を求めてください. 1y=(x+3)2−1 2y=(x−3)2−1 3y=4(x+3)2−1 4y=4(x−3)2−1 解説
x2の係数4は変わらず,頂点のx座標が3になり,y座標が−1になります.
y=4(x−3)2−1
→4
【問題2】
y=5(x−1)2+2のグラフを,x軸の正の向きに4,y軸の正の向きに3だけ平行移動してできるグラフの方程式を求めてください. 1y=5(x+4)2+3 2y=5(x−4)2+3 3y=5(x+5)2+5 4y=5(x−5)2+5 解説
x2の係数5は変わらず,頂点のx座標が1+4=5になり,y座標が2+3=5になります.
y=5(x−5)2+5
→4
【問題4】
y=3(x+1)2のグラフを,どちら向きに幾ら平行移動すればy=3x2+4のグラフにちょうど重なりますか. 1x軸の正の向きに−1,y軸の正の向きに−4 2x軸の正の向きに−1,y軸の正の向きに4 3x軸の正の向きに1,y軸の正の向きに−4 4x軸の正の向きに1,y軸の正の向きに4 解説
形は同じで,頂点のx座標を−1→0にするには+1,y座標を0→4にするには+4.
したがって,x軸の正の向きに1,y軸の正の向きに4だけ平行移動するとよい.
→4
|
|
【x=pの直線に関する対称移動:要点】
○[座標変換による方法]
(A) y=f(x)の形になっているとき
y=f(x)のグラフをx=pの直線に関して線対称移動してできるグラフの方程式は y=f(2p−x) になる. 【例】 …高校1年では習わない
元のグラフの方程式:y=4x3
x=1の直線に関して線対称移動 新しいグラフの方程式:y=4(2−x)3 (B) yについて解かれていないとき f(x, y)=0のグラフをx=pの直線に関して線対称移動してできるグラフの方程式は f(2p−x, y)=0 になる. 【例】 …高校1年では習わない
元のグラフの方程式:x2+y2=1(円)
x=1の直線に関して線対称移動 新しいグラフの方程式:(2−x)2+y2=1 (x−2)2+y2=1
≪この方法の強い所≫
…どんな形の関数に対しても使えること ≪この方法の弱い所≫ …高校1年生では難しいこと 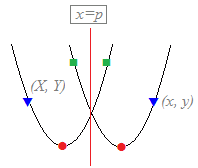 (解説)
(解説)(A) 元のグラフの方程式がy=f(x)であるときに,グラフ上の各点をx=pの直線(x軸に垂直,y軸に平行)に関して線対称移動してできるグラフの方程式は次のようにして求められる. 元の点(X, Y)はy=f(x)上にあるから,次の関係式を満たす
Y=f(X) …(1)
元の点(X, Y)をx=pの直線に関して線対称移動すると,新しい点(x, y)に移るのだから
=p …(2)
新しいグラフの方程式とは,新しい点(x, y)の満たすべき関係式のことだから,(1)(2)を使って元の座標(X, Y)を消去すればよい.y=Y (2)より
X=2p−x …(2’)
(2’)を(1)に代入するとY=y
y=f(2p−x) …(3)
(B) についても同様にして示せる.
f(x, y)=0 → f(2p−x, y)=0 …(4)
|
○[頂点の移動による方法]
(B) 元のグラフがy=a(x−m)2+nの形になっているとき 放物線y=a(x−m)2+nのグラフをx=pの直線に関して線対称移動してできるグラフは 形は同じだからx2の係数は変わらずa 頂点のx座標をsとおくと =p だから,s=2p−m 頂点のy座標は変わらずn y=a(x−(2p−m))2+n になる. 【例】
(1) 元のグラフの方程式:y=3(x−1)2+2
x=4の直線に関して線対称移動 (s=2p−mで求めてもよいが,算数的に1→4:+3だから4+3=7としてもよい) 新しいグラフの方程式:y=3(x−7)2+2
【問題5】
y=2(x−3)2+4のグラフを,x=5の直線に関して線対称移動してできるグラフの方程式を求めてください. 1y=2(x−5)2+4 2y=2(x−6)2+4 3y=2(x−7)2+4 4y=2(x−8)2+4 解説
3→5:+2だから5+2=7
頂点は(7, 4)になる
→3
【問題6】
y=−(x+6)2+3のグラフを,x=−2の直線に関して線対称移動してできるグラフの方程式を求めてください. 1y=−(x−2)2+3 2y=−(x+2)2+3 3y=(x−2)2−3 4y=(x+4)2−3 解説
−6→−2:+4だから−2+4=2
頂点は(2, 3)になる
→1
【問題7】
y=−3(x+2)2+5のグラフを,x軸に垂直な直線に関して線対称移動してy=−3(x−8)2+5とちょうど重なるようにするには,どのような直線に関して対称移動すればよいか. 1x=−6 2x=−3 3x=3 4x=6 解説
頂点は(−2, 5)→(8, 5)と移動するから,x軸に垂直な中央の線は
x==3
→3
|
|
【y=qの直線に関する対称移動:要点】
○[座標変換による方法]
(A) y=f(x)の形になっているとき
y=f(x)のグラフをy=qの直線に関して線対称移動してできるグラフの方程式は 2q−y=f(x) になる. 【例】 …高校1年では習わない
元のグラフの方程式:y=4x3
y=1の直線に関して線対称移動 新しいグラフの方程式:2−y=4x3 y=2−4x3 (B) yについて解かれていないとき f(x, y)=0のグラフをy=qの直線に関して線対称移動してできるグラフの方程式は f(x, 2q−y)=0 になる. 【例】 …高校1年では習わない
元のグラフの方程式:x2+y2=1(円)
y=1の直線に関して線対称移動 新しいグラフの方程式:x2+(y−2)2=1
≪この方法の強い所≫
…どんな形の関数に対しても使えること ≪この方法の弱い所≫ …高校1年生では難しいこと 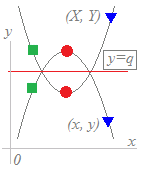 (解説)
(解説)(A) 元のグラフの方程式がy=f(x)であるときに,グラフ上の各点をy=qの直線(x軸に平行,y軸に垂直)に関して線対称移動してできるグラフの方程式は次のようにして求められる. 元の点(X, Y)はy=f(x)上にあるから,次の関係式を満たす
Y=f(X) …(1)
元の点(X, Y)をy=qの直線に関して線対称移動すると,新しい点(x, y)に移るのだから
x=X
=q …(2)
新しいグラフの方程式とは,新しい点(x, y)の満たすべき関係式のことだから,(1)(2)を使って元の座標(X, Y)を消去すればよい.(2)より
X=x
(2’)を(1)に代入するとY=2q−y …(2’)
2q−y=f(x) …(3)
(B) についても同様にして示せる.
f(x, y)=0 → f(x, 2q−y)=0 …(4)
|
○[頂点の移動による方法]
(B) 元のグラフがy=a(x−m)2+nの形になっているとき 放物線y=a(x−m)2+nのグラフをy=qの直線に関して線対称移動してできるグラフは 上下逆になるからx2の係数は符号が変わる→−a 頂点のx座標は変わらずm 頂点のy座標をtとおくと =q だから,t=2q−n y=−a(x−m)2+2q−n になる. 【例】
(1) 元のグラフの方程式:y=3(x−1)2+2
y=4の直線に関して線対称移動 (t=2q−nで求めてもよいが,算数的に2→4:+2だから4+2=6としてもよい) 新しいグラフの方程式:y=−3(x−1)2+6
【問題8】
y=3(x−4)2+5のグラフを,y=1の直線に関して線対称移動してできるグラフの方程式を求めてください. 1y=3(x+4)2+5 2y=3(x−4)2+5 3y=−3(x−4)2−3 4y=−3(x−4)2+3 解説
5→1:−4だから1−4=−3
頂点は(4, −3)になる 上下(凹凸)は逆になる. y=−3(x−4)2−3
→3
【問題9】
y=−2(x+3)2+4のグラフを,y=−1の直線に関して線対称移動してできるグラフの方程式を求めてください. 1y=2(x+3)2−6 2y=2(x+3)2+14 3y=−2(x+3)2−6 4y=−2(x+3)2+14 解説
4→−1:−5だから−1−5=−6
頂点は(−3, −6)になる 上下(凹凸)は逆になる. y=2(x+3)2−6
→1
|
|
【点(p, q)に関する点対称移動:要点】
○[座標変換による方法]
(A) y=f(x)の形になっているとき
y=f(x)のグラフを点(p, q)に関して点対称移動してできるグラフの方程式は 2q−y=f(2p−x) になる. 【例】 …高校1年では習わない
元のグラフの方程式:y=2x3
点(2, 3)に関して点対称移動 新しいグラフの方程式:6−y=2(4−x)3 y=6−2(4−x)3 y=6+2(x−4)3 (B) yについて解かれていないとき f(x, y)=0のグラフを点(p, q)に関して点対称移動してできるグラフの方程式は f(2p−x, 2q−y)=0 になる. 【例】 …高校1年では習わない
元のグラフの方程式:x2+y2=1(円)
点(2, 3)に関して点対称移動 新しいグラフの方程式:(4−x)2+(6−y)2=1 (x−4)2+(y−6)2=1
≪この方法の強い所≫
…どんな形の関数に対しても使えること ≪この方法の弱い所≫ …高校1年生では難しいこと 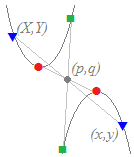 (解説)
(解説)(A) 元のグラフの方程式がy=f(x)であるときに,グラフ上の各点を点(p, q)に関して点対称移動してできるグラフの方程式は次のようにして求められる. 元の点(X, Y)はy=f(x)上にあるから,次の関係式を満たす
Y=f(X) …(1)
元の点(X, Y)を点(p, q)に関して点対称移動すると,新しい点(x, y)に移るのだから
=p …(2)
新しいグラフの方程式とは,新しい点(x, y)の満たすべき関係式のことだから,(1)(2)を使って元の座標(X, Y)を消去すればよい.=q (2)より
X=2p−x
(2’)を(1)に代入するとY=2q−y …(2’)
2q−y=f(2p−x) …(3)
(B) についても同様にして示せる.
f(x, y)=0 → f(2p−x, 2q−y)=0 …(4)
|
○[頂点の移動による方法]
(B) 元のグラフがy=a(x−m)2+nの形になっているとき 放物線y=a(x−m)2+nのグラフを点(p, q)に関して点対称移動してできるグラフは 上下逆になるからx2の係数は符号が変わる→−a 頂点のx座標をsとおくと 頂点のy座標をtとおくと =p だから,s=2p−m =q だから,t=2q−n y=−a(x−(2p−m))2+2q−n になる. 【例】
(1) 元のグラフの方程式:y=3(x−1)2+2
点(4, 6)に関して点対称移動 (s=2p−m, t=2q−nで求めてもよいが,算数的に(1, 2)→(4, 6):(+3, +4)だから(4+3,6+4)=(7, 10)としてもよい) 新しいグラフの方程式:y=−3(x−7)2+10
【問題10】
y=4(x−3)2+5のグラフを,点(1, 0)に関して点対称移動してできるグラフの方程式を求めてください. 1y=−4(x+1)2−5 2y=4(x+1)2−5 3y=−4(x−1)2−5 4y=4(x−1)2+5 解説
(3,5)→(1,0):(−2,−5)だから(1−2,0−5)=(−1,−5)
頂点は(−1, −5)になる 上下(凹凸)は逆になる. y=−4(x+1)2−5
→1
【問題11】
y=−2x2−3のグラフを,点(−4, 1)に関して点対称移動してできるグラフの方程式を求めてください. 1y=2(x−8)2+5 2y=2(x+8)2+5 3y=−2(x−8)2−5 4y=−2(x+8)2+5 解説
(0,−3)→(−4,1):(−4,+4)だから(−4−4,1+4)=(−8,5)
頂点は(−8, 5)になる 上下(凹凸)は逆になる. y=2(x+8)2+5
→2
|
|
【問題12】
y=−(x−2)2+1のグラフを,x=−1の直線に関して対称移動してから,さらに,y=2に関して対称移動してできるグラフの方程式を求めてください. 1y=−(x+4)2+3 2y=(x+4)2+3 3y=−x2+3 4y=x2+3 解説
頂点は(2,1)→(−4,1)→(−4,3)と移動します
上下(凹凸)は逆になります. y=(x+4)2+3
→2
【問題14】
元のグラフy=−(x−2)2+3を,x軸方向に−2,y軸方向に−4だけ平行移動してから,さらに点(−1, 2)に関して対称移動すると,元のグラフを点(−1, 2)に関して対称移動してから,x軸方向にp,y軸方向にqだけ平行移動したグラフと一致する. 上記のp, qの値を求めてください. 1p=1, q=2 2p=2, q=4 3p=−1, q=−2 4p=−2, q=−4 解説
初めの移動方法で,頂点は(2,3)→(0,−1)→(−2,5)と移動します.
後の移動方法では,頂点は(2,3)→(−4,1)→(−2,5)と移動します. 上下(凹凸)は同じ→逆,逆→同じで,いずれも逆になります. (−4,1)→(−2,5)の移動は,x軸方向に2,y軸方向に4の平行移動になります.
→2
|
【問題13】
元のグラフy=(x+3)2+2を,点(−1, 0)に関して対称移動してから,さらに点(2, 1)に関して対称移動すると,元のグラフをx軸方向にp,y軸方向にqだけ平行移動したグラフと一致する. 上記のp, qの値を求めてください. 1p=3, q=2 2p=3, q=4 3p=6, q=4 4p=6, q=2 解説
頂点は(−3,2)→(1,−2)→(3,4)と移動します.
上下(凹凸)は逆の逆で元に戻ります. したがって,x軸方向に6,y軸方向に2だけ平行移動したグラフと一致します.
→4
【問題15】
y=a(x−m)2+nのグラフを次の(A)→(B)の順に移動した結果と(B)→(A)の順に移動した結果がつねに一致するものを選んでください. 1 (A) x方向にp,y方向にqだけ平行移動する (B) 点(c,d )に関して対称移動する 2 (A) x=cの直線に関して対称移動する (B) x方向にp,y方向にqだけ平行移動する 3 (A) x=pの直線に関して対称移動する (B) y=qの直線に関して対称移動する 4 (A) 点(c, d)に関して対称移動する (B) 点(e, f)に関して対称移動する 解説 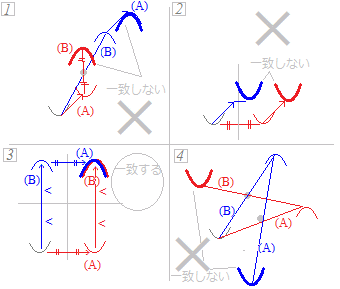 式で示すこともできますが,示すべき式の分量が多くて大変になります.
→3
|